Question

如图，帆船A和帆船B在太湖湖面上训练，O为湖面上的一个定点，教练船静候于点O，训练时要求A、B两船始终关于O点对称．以O为原点，建立如图所示的坐标系，x轴、y轴的正方向分别表示正东、正北方向．设A、B两船可近似看成在双曲线y=

4

x

上运动，湖面风平浪静，双帆远影优美，训练中档教练船与A、B两船恰好在直线y=x上时，三船同时发现湖面上有一遇险的C船，此时教练船测得C船在东南45°方向上，A船测得AC与AB的夹角为60°，B船也同时测得C船的位置（假设C船位置不再改变，A、B、C三船可分别用A、B、C三点表示）．
（1）发现C船时，A、B、C三船所在位置的坐标分别为A（

 

，

 

）、B（

 

，

 

）和C（

 

，

 

）；
（2）发现C船，三船立即停止训练，并分别从A、O、B三点出发沿最短路线同时前往救援，设A、B两船的速度相等，教练船与A船的速度之比为3：4，问教练船是否最先赶到？请说明理由．

Answer 1

分析：（1）A、B两点直线y=x上和双曲线y=

4

x

，列方程组可求A、B两点坐标，在依题意判断△ABC为等边三角形，OA=2

2

，则OC=

3

OA=2

6

，过C点作x轴的垂线CE，垂足为E，利用OC在第四象限的角平分线上求OE，CE，确定C点坐标；
（2）分别求出AC、OC的长，分别表示教练船与A、B两船的速度与时间，比较时间的大小即可．

解答：解：（1）CE⊥x轴于E，解方程组

y=x y= 4 x

得

x1=2 y1=2

，

x2=-2 y2=-2

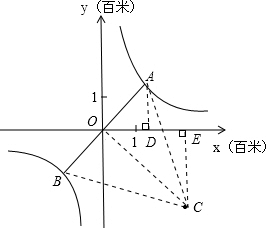
∴A（2，2），B（-2，-2），
在等边△ABC中可求OA=2

2

，
则OC=

3

OA=2

6

，
在Rt△OCE中，OE=CE=OC•sin45°=2

3

，
∴C（2

3

，-2

3

）；

（2）作AD⊥x轴于D，连AC、BC和OC，
∵A（2，2），
∴∠AOD=45°，AO=2

2

，
∵C在O的东南45°方向上，
∴∠AOC=45°+45°=90°，
∵AO=BO，∴AC=BC，
又∵∠BAC=60°，
∴△ABC为正三角形，
∴AC=BC=AB=2AO=4

2

，
∴OC=

3

2

•4

2

=2

6

，
由条件设教练船的速度为3m，A、B两船的速度都为4m，
则教练船所用时间为

2 6

3m

，A、B两船所用时间均为

4 2

4m

=

2

m

，
∵

2 6

3m

=

24

3m

，

2

m

=

18

3m

，
∴

2 6

3m

＞

2

m

；
∴教练船没有最先赶到．

点评：本题考查了直角坐标系中点的求法，根据点的坐标求两点之间距离的方法．解答本题时同学们要读懂题意，就不易出错．