题目内容
设A△B=AB+A+B,如2△3=2×3+2+3=11,那么((1△9)△9)△9=________.(…((1△9)△9)△9…)△9(一共n个9)=________.(n为正整数)
1999 199…99(共n个9)
分析:根据A△B=AB+A+B可以得到A△B=AB+A+B=(A+1)(B+1)-1,然后进行计算即可.
解答:∵A△B=AB+A+B=(A+1)(B+1)-1∴((1△9)△9)△9={[(1+1)(9+1)-1]△9}△9=(19△9)△9=[(19+1)(9+1)-1]△9=199△9=(199+1)(9+1)-1=1999 (…((1△9)△9)…)△9=199…99(共n个9).
故答案为1999,199…99(共n个9).
点评:本题考查了数字规律类题目,解题的关键是仔细地观察题目提供的例子并从中找到正确的规律,并利用此规律解题.
分析:根据A△B=AB+A+B可以得到A△B=AB+A+B=(A+1)(B+1)-1,然后进行计算即可.
解答:∵A△B=AB+A+B=(A+1)(B+1)-1∴((1△9)△9)△9={[(1+1)(9+1)-1]△9}△9=(19△9)△9=[(19+1)(9+1)-1]△9=199△9=(199+1)(9+1)-1=1999 (…((1△9)△9)…)△9=199…99(共n个9).
故答案为1999,199…99(共n个9).
点评:本题考查了数字规律类题目,解题的关键是仔细地观察题目提供的例子并从中找到正确的规律,并利用此规律解题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
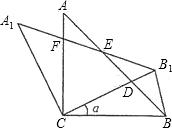 明(△ABC与△A1B1C1全等除外);
明(△ABC与△A1B1C1全等除外);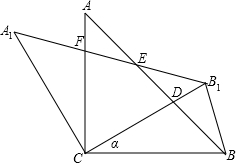
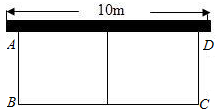 篱笆,一面靠墙(墙长为10 m),设花圃宽AB为x(m),面积为S(m2).
篱笆,一面靠墙(墙长为10 m),设花圃宽AB为x(m),面积为S(m2).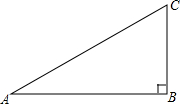 (2013•黔东南州)如图,在直角三角形ABC中,∠ABC=90°.
(2013•黔东南州)如图,在直角三角形ABC中,∠ABC=90°.