题目内容
【题目】仔细观察图形，认真分析下列各式，然后解答问题.
OA
＝(
)2＋1＝2，S1＝
；
OA
＝(
)2＋1＝3，S2＝
；
OA
＝(
)2＋1＝4，S3＝
；
…
求：(1)请用含有n(n是正整数)的等式表示上述变化规律；
(2)推算出OA10的长；
(3)求出S
＋S＋S＋…＋S
的值．
【答案】(1) 
,Sn＝
(n为正整数)；（2）
；（3）
.
【解析】
（1）根据题意可知当n为正整数时，OAn2=（
）2+1，Sn=
；
（2）把n=10，代入到（1）所推出的结论即可求出OA10的值；
（3）把n=1，2，3…10，分别代入到（1）所推出的结论Sn=，即可求出S12，S22，S32，…S102的值，即可推出结果．
解：(1)
＝()2＋1＝n，Sn＝(n为正整数)．
(2)∵
＝10，
∴OA10＝；
(3) S12＋S22＋S32＋…＋S102
＝(
)2＋(
)2＋(
)2＋…＋(
)2＋(
)2
＝
＋
＋
＋…＋
＋
＝
＝
＝.
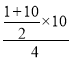
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
