题目内容
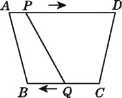
【题目】操作与思考:一张边长为a的正方形桌面,因为实际需要,需将正方形边长增加b,从而得到一个更大的正方形,木工师傅设计了如图所示的方案:
(1)方案中大正方形的边长都是 ,所以面积为 ;
(2)小明还发现:方案中大正方形的面积还可以用四块小四边形的面积和来表示 ;
(3)你有什么发现,请用数学式子表达 ;
(4)利用(3)的结论计算20.182+2×20.18×19.82+19.822的值.

【答案】(1) (a+b),(a+b)2;(2) (a2+2ab+b2);(3) (a+b)2=a2+2ab+b2;(4)1600
【解析】
(1)根据图形得出正方形的边长,再利用正方形的面积公式即可得;
(2)将四个小四边形的面积相加,再合并同类项即可得;
(3)由大正方形面积不变可得等式;
(4)利用所得等式将原式变形为(20.18+19.82)2,再进一步计算可得.
解:(1)方案中大正方形的边长都是(a+b),所以面积为(a+b)2,
故答案为:(a+b),(a+b)2;
(2)方案中大正方形的面积还可以用四块小四边形的面积和来表示:a2+ab+ab+b2=a2+2ab+b2,
故答案为:(a2+2ab+b2);
(3)根据大正方形的面积不变可知(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2.
(4)20.182+2×20.18×19.82+19.822
=(20.18+19.82)2
=402
=1600.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案【题目】某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
【题目】某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为x(0<x<0.5).
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ① |
平均步长(米/步) | 0.6 | ② |
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.