题目内容
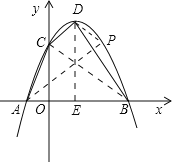
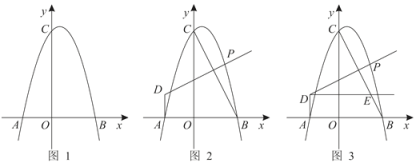
【题目】已知:如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,3),与x轴交于A、B两点,点A的坐标为(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)设点P是在第一象限内抛物线上的一个动点,求使与四边形ACDB面积相等的四边形ACPB的点P的坐标;
(3)求△APD的面积.
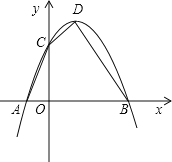
【答案】(1)y=-x2+2x+3,(1,4);(2)点P的坐标是(2,3);(3)△APD的面积是3.
【解析】
(1)根据抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,3),与x轴交于A(-1,0),代入即可求出a、c的值,即得到解析式,化成顶点式就能求出顶点坐标;
(2)连接BC,过点D作DE⊥x轴于点E,令y=0,求出B的坐标,根据点的坐标和面积公式能求出四边形ACDB和△BCD的面积,根据B、C的坐标能求出直线BC,设直线DP的函数解析式为y=-x+b,把点D(1,4)代入即可求出直线DP的函数解析式,求出y=-x+5和y=-x2+2x+3组成的方程组的解即可;
(3)根据对称得到△APD≌△BCD,根据全等三角形的性质即可得到答案.
(1)∵抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,3),与x轴
交于A(-1,0)
∴
![]() ,
,
解得
![]() ,
,
∴抛物线的解析式为y=-x2+2x+3,
∵y=-(x2-2x)+3=-(x2-2x+1-1)+3=-(x-1)2+4,
∴顶点D的坐标为(1,4),
答:抛物线的解析式是y=-x2+2x+3,顶点D的坐标是(1,4).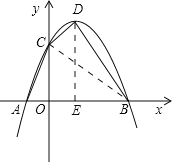
(2)连接BC,过点D作DE⊥x轴于点E.
令y=0则-x2+2x+3=0,
∴x1=-1,x2=3
∴点B的坐标为(3,0),
∴S四边形ACDB=S△AOC+S梯形OEDC+S△EBD=![]() ×1×3+
×1×3+![]() ×(3+4)×1+
×(3+4)×1+![]() ×2×4=9
×2×4=9
∵S△ABC=![]() ×4×3=6
×4×3=6
∴S△BCD=3
∵点P是在第一象限内抛物线上的一个动点,S四边形ACDB=S四边形ACPB,
∴S△BCP=S△BCD=3,
∴点P是过D且与直线BC平行的直线和抛物线的交点,
而直线BC的函数解析式为y=-x+3,
∴设直线DP的函数解析式为y=-x+b,过点D(1,4),
∴-1+b=4,b=5,
∴直线DP的函数解析式为y=-x+5,
把y=-x+5代入y=-x2+2x+3中,解得x1=1,x2=2,
∴点P的坐标为(2,3),
答:与四边形ACDB面积相等的四边形ACPB的点P的坐标是(2,3).
(3)∵点P与点C关于DE对称,点B与点A关于DE对称,
∴△APD≌△BCD,
∴S△APD=S△BCD=3,
答:△APD的面积是3.