题目内容
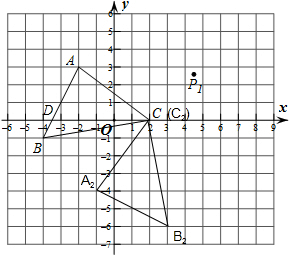
(2012•武汉模拟)在平面直角坐标系中,△ABC的顶点坐标是A(-2,3),B(-4,-1),C(2,0).点P (m,n)为△ABC内一点,平移△ABC得到△A1B1C1,使点P(m,n)移到P(m+6,n+1)处.
(m,n)为△ABC内一点,平移△ABC得到△A1B1C1,使点P(m,n)移到P(m+6,n+1)处.
(1)请直接写出点A1,B1,C1的坐标;
(2)将△ABC绕坐标点C逆时针旋转90°得到△A2B2C,画出△A2B2C;
(3)直接写出△ABC的面积.
 (m,n)为△ABC内一点,平移△ABC得到△A1B1C1,使点P(m,n)移到P(m+6,n+1)处.
(m,n)为△ABC内一点,平移△ABC得到△A1B1C1,使点P(m,n)移到P(m+6,n+1)处.(1)请直接写出点A1,B1,C1的坐标;
(2)将△ABC绕坐标点C逆时针旋转90°得到△A2B2C,画出△A2B2C;
(3)直接写出△ABC的面积.
分析:(1)根据P(m,n)移到P(m+6,n+1)可知△ABC向左平移6个单位,向上平移了一个单位,由图形平移的性质即可得出出点A1,B1,C1的坐标;
(2)根据图形旋转的性质画出旋转后的图形即可;
(3)先设线段AB与x轴交于点D,根据A、B两点坐标求出直线AB的解析式,进而可得出D点坐标,由S△ABC=S△ACD+S△BCD进行计算即可.
(2)根据图形旋转的性质画出旋转后的图形即可;
(3)先设线段AB与x轴交于点D,根据A、B两点坐标求出直线AB的解析式,进而可得出D点坐标,由S△ABC=S△ACD+S△BCD进行计算即可.
解答:解:(1)∵平移△ABC得到△A1B1C1,点P(m,n)移到P(m+6,n+1)处,
∴△ABC向左平移6个单位,向上平移了一个单位,
∴A1(4,4),B1(2,0),C1(8,1);
(2)如图所示:
(3)设线段AB与x轴交于点D,设过AB两点的直线解析式为:y=kx+b(k≠0)
∵A(-2,3),B(-4,-1),
∴
,解得
,
∴过AB两点的直线解析式为:y=2x+7,
∴D(-
,0),
∴DC=
+2=
∴S△ABC=S△ACD+S△BCD=
×
×3+
×
×1=11.
∴△ABC向左平移6个单位,向上平移了一个单位,
∴A1(4,4),B1(2,0),C1(8,1);
(2)如图所示:

(3)设线段AB与x轴交于点D,设过AB两点的直线解析式为:y=kx+b(k≠0)
∵A(-2,3),B(-4,-1),
∴
|
|
∴过AB两点的直线解析式为:y=2x+7,
∴D(-
| 7 |
| 2 |
∴DC=
| 7 |
| 2 |
| 11 |
| 2 |
∴S△ABC=S△ACD+S△BCD=
| 1 |
| 2 |
| 11 |
| 2 |
| 1 |
| 2 |
| 11 |
| 2 |
点评:本题考查的是旋转变换及平移变换,熟知图形旋转或平移后所得图形与原图形全等是解答此题的关键.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 (2012•武汉模拟)小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1,l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则x=
(2012•武汉模拟)小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1,l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则x= (2012•武汉模拟)如图,在平面直角坐标系的第一象限中有一个5×5的方形网格,每个小正方形的边长皆为1个单位长,反比例函数
(2012•武汉模拟)如图,在平面直角坐标系的第一象限中有一个5×5的方形网格,每个小正方形的边长皆为1个单位长,反比例函数 (2012•武汉模拟)医药研究所试验某种新药药效时,成人如果按剂量服用,血液中每毫升含药量y(毫克)随时间x的变化如图所示,如果每毫升血液中含药量超过4微克(含4微克)时治疗疾病为有效,那么有效时间是
(2012•武汉模拟)医药研究所试验某种新药药效时,成人如果按剂量服用,血液中每毫升含药量y(毫克)随时间x的变化如图所示,如果每毫升血液中含药量超过4微克(含4微克)时治疗疾病为有效,那么有效时间是