题目内容
 (2013•眉山)如图,在函数y1=
(2013•眉山)如图,在函数y1=| k1 |
| x |
| k2 |
| x |
| 1 |
| 2 |
| 9 |
| 2 |
10
| ||
| 3 |
10
| ||
| 3 |
分析:根据反比例函数y=
(k≠0)系数k的几何意义易得两反比例解析式为y=-
,y=
,设B点坐标为(
,t)(t>0),则可表示出A点坐标为(-
,t),然后证明Rt△AOC∽Rt△OBC,得到OC:BC=AC:OC,即t:
=
:t,解得t=
,再确定A、B点的坐标,最后用两点的横坐标之差来得到线段AB的长.
| k |
| x |
| 1 |
| x |
| 9 |
| x |
| 9 |
| t |
| 1 |
| t |
| 9 |
| t |
| 1 |
| t |
| 3 |
解答:解:∵S△AOC=
,S△BOC=
,
∴
|k1|=
,
|k2|=
,
∴k1=-1,k2=9,
∴两反比例解析式为y=-
,y=
,
设B点坐标为(
,t)(t>0),
∵AB∥x轴,
∴A点的纵坐标为t,
把y=t代入y=-
得x=-
,
∴A点坐标为(-
,t),
∵OA⊥OB,
∴∠AOC=∠OBC,
∴Rt△AOC∽Rt△OBC,
∴OC:BC=AC:OC,即t:
=
:t,
∴t=
,
∴A点坐标为(-
,
),B点坐标为(3
,
),
∴线段AB的长度=3
-(-
)=
.
故答案为
.
| 1 |
| 2 |
| 9 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∴k1=-1,k2=9,
∴两反比例解析式为y=-
| 1 |
| x |
| 9 |
| x |
设B点坐标为(
| 9 |
| t |
∵AB∥x轴,
∴A点的纵坐标为t,
把y=t代入y=-
| 1 |
| x |
| 1 |
| t |
∴A点坐标为(-
| 1 |
| t |
∵OA⊥OB,
∴∠AOC=∠OBC,
∴Rt△AOC∽Rt△OBC,
∴OC:BC=AC:OC,即t:
| 9 |
| t |
| 1 |
| t |
∴t=
| 3 |
∴A点坐标为(-
| ||
| 3 |
| 3 |
| 3 |
| 3 |
∴线段AB的长度=3
| 3 |
| ||
| 3 |
10
| ||
| 3 |
故答案为
10
| ||
| 3 |
点评:本题考查了反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y=
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
| k |
| x |
| k |
| x |

练习册系列答案
相关题目
 (2013•眉山)如图,△ABC中,E、F分别是AB、AC上的两点,且
(2013•眉山)如图,△ABC中,E、F分别是AB、AC上的两点,且 (2013•眉山)如图是小强用八块相同的小正方体搭建的一个积木,它的左视图是( )
(2013•眉山)如图是小强用八块相同的小正方体搭建的一个积木,它的左视图是( ) (2013•眉山)如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:
(2013•眉山)如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论: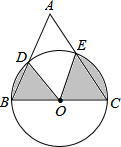 (2013•眉山)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为
(2013•眉山)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为