题目内容
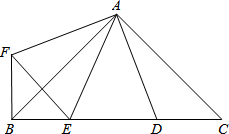 (2013•眉山)如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:
(2013•眉山)如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF;②△ABE∽△ACD;③BE+DC>DE;④BE2+DC2=DE2,
其中正确的有( )个.
分析:根据∠DAF=90°,∠DAE=45°,得出∠FAE=45°,利用SAS证明△AED≌△AEF,判定①正确;
如果△ABE∽△ACD,那么∠BAE=∠CAD,由∠ABE=∠C=45°,则∠AED=∠ADE,AD=AE,而由已知不能得出此条件,判定②错误;
先由∠BAC=∠DAF=90°,得出∠CAD=∠BAF,再利用SAS证明△ACD≌△ABF,得出CD=BF,又①知DE=EF,那么在△BEF中根据三角形两边之和大于第三边可得BE+BF>EF,等量代换后判定③正确;
先由△ACD≌△ABF,得出∠C=∠ABF=45°,进而得出∠EBF=90°,然后在Rt△BEF中,运用勾股定理得出BE2+BF2=EF2,等量代换后判定④正确.
如果△ABE∽△ACD,那么∠BAE=∠CAD,由∠ABE=∠C=45°,则∠AED=∠ADE,AD=AE,而由已知不能得出此条件,判定②错误;
先由∠BAC=∠DAF=90°,得出∠CAD=∠BAF,再利用SAS证明△ACD≌△ABF,得出CD=BF,又①知DE=EF,那么在△BEF中根据三角形两边之和大于第三边可得BE+BF>EF,等量代换后判定③正确;
先由△ACD≌△ABF,得出∠C=∠ABF=45°,进而得出∠EBF=90°,然后在Rt△BEF中,运用勾股定理得出BE2+BF2=EF2,等量代换后判定④正确.
解答:解:①∵∠DAF=90°,∠DAE=45°,
∴∠FAE=∠DAF-∠DAE=45°.
在△AED与△AEF中,
,
∴△AED≌△AEF(SAS),①正确;
②∵∠BAC=90°,AB=AC,
∴∠ABE=∠C=45°.
∵点D、E为BC边上的两点,∠DAE=45°,
∴AD与AE不一定相等,∠AED与∠ADE不一定相等,
∵∠AED=45°+∠BAE,∠ADE=45°+∠CAD,
∴∠BAE与∠CAD不一定相等,
∴△ABE与△ACD不一定相似,②错误;
③ ∵∠BAC=∠DAF=90°,
∵∠BAC=∠DAF=90°,
∴∠BAC-∠BAD=∠DAF-∠BAD,即∠CAD=∠BAF.
在△ACD与△ABF中,
,
∴△ACD≌△ABF(SAS),
∴CD=BF,
由①知△AED≌△AEF,
∴DE=EF.
在△BEF中,∵BE+BF>EF,
∴BE+DC>DE,③正确;
④由③知△ACD≌△ABF,
∴∠C=∠ABF=45°,
∵∠ABE=45°,
∴∠EBF=∠ABE+∠ABF=90°.
在Rt△BEF中,由勾股定理,得BE2+BF2=EF2,
∵BF=DC,EF=DE,
∴BE2+DC2=DE2,④正确.
所以正确的结论有①③④.
故选C.
∴∠FAE=∠DAF-∠DAE=45°.
在△AED与△AEF中,
|
∴△AED≌△AEF(SAS),①正确;
②∵∠BAC=90°,AB=AC,
∴∠ABE=∠C=45°.
∵点D、E为BC边上的两点,∠DAE=45°,
∴AD与AE不一定相等,∠AED与∠ADE不一定相等,
∵∠AED=45°+∠BAE,∠ADE=45°+∠CAD,
∴∠BAE与∠CAD不一定相等,
∴△ABE与△ACD不一定相似,②错误;
③
 ∵∠BAC=∠DAF=90°,
∵∠BAC=∠DAF=90°,∴∠BAC-∠BAD=∠DAF-∠BAD,即∠CAD=∠BAF.
在△ACD与△ABF中,
|
∴△ACD≌△ABF(SAS),
∴CD=BF,
由①知△AED≌△AEF,
∴DE=EF.
在△BEF中,∵BE+BF>EF,
∴BE+DC>DE,③正确;
④由③知△ACD≌△ABF,
∴∠C=∠ABF=45°,
∵∠ABE=45°,
∴∠EBF=∠ABE+∠ABF=90°.
在Rt△BEF中,由勾股定理,得BE2+BF2=EF2,
∵BF=DC,EF=DE,
∴BE2+DC2=DE2,④正确.
所以正确的结论有①③④.
故选C.
点评:本题考查了勾股定理,全等三角形的判定与性质,等腰直角直角三角形的性质,三角形三边关系定理,相似三角形的判定,此题涉及的知识面比较广,解题时要注意仔细分析,有一定难度.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 (2013•眉山)如图,△ABC中,E、F分别是AB、AC上的两点,且
(2013•眉山)如图,△ABC中,E、F分别是AB、AC上的两点,且 (2013•眉山)如图是小强用八块相同的小正方体搭建的一个积木,它的左视图是( )
(2013•眉山)如图是小强用八块相同的小正方体搭建的一个积木,它的左视图是( ) (2013•眉山)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为
(2013•眉山)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为 (2013•眉山)如图,在函数y1=
(2013•眉山)如图,在函数y1=