题目内容
【题目】如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF 
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.
【答案】
(1)解:证明:∵四边形ABCD和四边形DEFG都是正方形,
∴AD=CD,ED=GD,FE=FG.
∴AD﹣ED=CD﹣GD.
∴AE=CG.
在△AFE和△CFG中
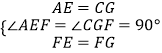 ,
,
∴△AFE≌△CFG(SAS),
∴AF=CF;
(2)解:解:由(1)得△AEF≌△CGF,
∴∠AFE=∠CFG.
又∵AB∥EF,∠BAF=35°,
∴∠AFE=∠CFG=∠BAF=35°.
连接DF,
∵四边形DEFG是正方形,
∴∠DFG=45°.
∴∠BFC=180°﹣∠CFG﹣∠GFD=180°﹣35°﹣45°=100°.
即∠BFC=100°.
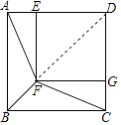
【解析】(1)利用正方形的性质结合全等三角形的判定与性质得出△AFE≌△CFG进而得出AF=CF;(2)利用正方形的对角线平分对角进而得出答案.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.

练习册系列答案
相关题目
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克) |
|
|
|
|
|
|
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐重______千克;
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价![]() 元,则出售这20筐白菜可卖多少元?
元,则出售这20筐白菜可卖多少元?