��Ŀ����
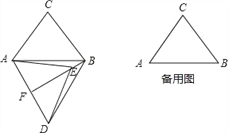
����Ŀ���ڡ�ABC��,AB=6,AC=BC=5,����ABC�Ƶ�A��˳ʱ�뷽����ת,�õ���ADE,��ת��Ϊ����0�㣼����180�㣩,��B�Ķ�Ӧ��Ϊ��D,��C�Ķ�Ӧ��Ϊ��E,����BD��BE��
��1����ͼ,����=60��ʱ,�ӳ�BE��AD�ڵ�F��
����֤����ABD�ǵȱ������Σ�
����֤��BF��AD��AF=DF��
����ֱ��д��BE�ij���
��2������ת������,����D��DG��ֱ��ֱ��AB,����Ϊ��G,����CE,����DAG=��ACB,���߶�DG���߶�AE������ʱ,��ֱ��д��BE+CE��ֵ��
���𰸡���1���٢������������3![]() ��4����2��13��
��4����2��13��
�������������������1��������ת����֪AB=AD����BAD=60�����ɵ�֤������BA=BD��EA=ED�����д������ʼ��ɵ�֤�����ֱ����BF��EF�ij����ɵã���2������ACB+��BAC+��ABC=180������DAG+��DAE+��BAE=180������DAG=��ACB����DAE=��BAC����BAE=��BAC��AE=AC���������ߺ�һ�ɵ�CE��AB��AC=5��AH=3���̶�֪CE=2CH=8��BE=5�����ɵô𰸣�
�����������1���١ߡ�ABC�Ƶ�A˳ʱ�뷽����ת60���õ���ADE��
��AB=AD����BAD=60����
���ABD�ǵȱ������Σ�
����������ABD�ǵȱ������Σ�
��AB=BD��
�ߡ�ABC�Ƶ�A˳ʱ�뷽����ת60���õ���ADE��
��AC=AE��BC=DE��
����AC=BC��
��EA=ED��
����B��E��AD���д����ϣ�
��BE��AD���д��ߣ�
����F��BE���ӳ����ϣ�
��BF��AD�� AF=DF��
������֪BF��AD��AF=DF��
��AF=DF=3��
��AE=AC=5��
��EF=4��
���ڵȱ�������ABD�У�BF=ABsin��BAF=6��![]() =3
=3![]() ��
��
��BE=BF��EF=3![]() ��4��
��4��
��2����ͼ��ʾ��
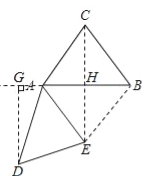
�ߡ�DAG=��ACB����DAE=��BAC��
���ACB+��BAC+��ABC=��DAG+��DAE+��ABC=180����
���ߡ�DAG+��DAE+��BAE=180����
���BAE=��ABC��
��AC=BC=AE��
���BAC=��ABC��
���BAE=��BAC��
��AB��CE����CH=HE=![]() CE��
CE��
��AC=BC��
��AH=BH=![]() AB=3��
AB=3��
��CE=2CH=8��BE=5��
��BE+CE=13��

 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�