题目内容
(11·大连)(本题9分)如图9,AB是⊙O的直径,CD是⊙O的切线,切点
为C,BE⊥CD,垂足为E,连接AC、BC.
(1)△ABC的形状是______________,理由是_________________;
(2)求证:BC平分∠ABE;
(3)若∠A=60°,OA=2,求CE的长.
解:(1)直角三角形;
直径所对的圆周角是直角,有一个角是直角的三角形是直角三角形.…………………2分
(2)连接OC,∵CD是⊙O的切线,
∴OC⊥CD
∴∠OCB+∠BCE=90°
∵BE⊥CD,
∴∠CBE+∠BCE=90°
∴∠OCB=∠CBE,…………………………4分
又∵且OC=OB,
∴∠OCB=∠OBC…………………………5分
∴∠EBC=∠OBC,即BC平分∠ABE;…………………………6分
(3)在Rt△ABC中,BC=AB·sinA=2×2×sin60°=,
在Rt△BCE中,∵∠CBE=∠ABC=90°-∠A=30°
解析:略

练习册系列答案
相关题目
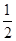 ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.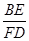 的值(用含k的式子表示).
的值(用含k的式子表示).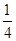 (容器各面的厚
(容器各面的厚