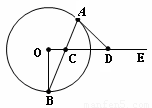
题目内容
如图,C是射线 OE上的一动点,AB是过点 C的弦,直线DA与OE的交点为D,现有三个论断: ①DA是⊙O的切线;②DA=DC;③ OD⊥OB.请你以其中的两个论断为条件,另一个论断为结论,用序号写出一个真命题,
用“★★
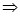 ★”表示.并给出证明;我的命题是: .
★”表示.并给出证明;我的命题是: .
我的命题是:①②?③解析:
证明:连接OA,则OA⊥DA,
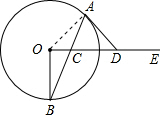
∵DA=DC,∴∠DAC=∠DCA,
∵OA=OB,∴∠B=∠OAB;∵∠OAB+∠DAC=90°,又∵∠OCB=∠DCA,∴∠B+∠OCB=90°,∴BO⊥CO.(其它方法酌情给分)
本题主要考查了切线的性质,根据等角的余角相等,等边对等角进行求解是本题的基本思路
证明:连接OA,则OA⊥DA,

∵DA=DC,∴∠DAC=∠DCA,
∵OA=OB,∴∠B=∠OAB;∵∠OAB+∠DAC=90°,又∵∠OCB=∠DCA,∴∠B+∠OCB=90°,∴BO⊥CO.(其它方法酌情给分)
本题主要考查了切线的性质,根据等角的余角相等,等边对等角进行求解是本题的基本思路

练习册系列答案
相关题目
 24、如图,C是射线OE上的一动点,AB是过点C的弦,直线DA与OE的交点为D,现有三个论断:①DA是⊙O的切线;②DA=DC;③OD⊥OB.请你以其中的两个论断为条件,另一个论断为结论,用序号写出一个真命题,用“★★?★”表示.并给出证明.我的命题是:
24、如图,C是射线OE上的一动点,AB是过点C的弦,直线DA与OE的交点为D,现有三个论断:①DA是⊙O的切线;②DA=DC;③OD⊥OB.请你以其中的两个论断为条件,另一个论断为结论,用序号写出一个真命题,用“★★?★”表示.并给出证明.我的命题是:
 ○”表示。并证明。
○”表示。并证明。
 ○”表示。并证明。
○”表示。并证明。 ★”表示.并给出证明;我的命题是:
.
★”表示.并给出证明;我的命题是:
.