题目内容
 如图,直线y=
如图,直线y=| 1 |
| 2 |
(2
,
)(-4,8)(5,
)
| 5 |
| 5 |
| 5 |
| 2 |
(2
,
)(-4,8)(5,
)
.| 5 |
| 5 |
| 5 |
| 2 |
分析:根据OB为菱形的对角线,OB为菱形的边两种情况,分别求出符合条件的N点坐标.
解答:解:①当OB为菱形的对角线时,如图1,由OB=5可知,M点纵坐标为
,
代入直线y=
x+5中,得M点横坐标为-5,
∵M、N关于y轴对称,∴N(5,
);

②当OB为菱形的边时,如图2,
延长MN交x轴于P点,
∵OA=10,OB=5,
∴AB=
=5
,
而ON=5,由△OPN∽△AOB,
得
=
=
,即
=
=
,
解得OP=2
,PN=
,
∴N(2
,
),
同理可得N′(-4,8).

故答案为:(2
,
)(-4,8)(5,
).
| 5 |
| 2 |
代入直线y=
| 1 |
| 2 |
∵M、N关于y轴对称,∴N(5,
| 5 |
| 2 |

②当OB为菱形的边时,如图2,
延长MN交x轴于P点,
∵OA=10,OB=5,
∴AB=
| OA2+OB2 |
| 5 |
而ON=5,由△OPN∽△AOB,
得
| OP |
| AO |
| PN |
| OB |
| ON |
| AB |
| OP |
| 10 |
| PN |
| 5 |
| 5 | ||
5
|
解得OP=2
| 5 |
| 5 |
∴N(2
| 5 |
| 5 |
同理可得N′(-4,8).

故答案为:(2
| 5 |
| 5 |
| 5 |
| 2 |
点评:本题考查了一次函数的综合运用,一次函数图象上点的坐标特点,菱形的性质.关键是根据OB为菱形的对角线,菱形的边,分类求解.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图,直线y=-
如图,直线y=- D为直径作⊙A交CD于F,FA的延长线交⊙A于E,交x轴于B.
D为直径作⊙A交CD于F,FA的延长线交⊙A于E,交x轴于B. 如图,直线y=-
如图,直线y=-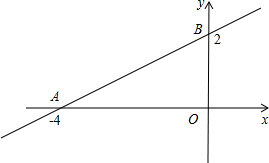 如图,直线y=
如图,直线y= (2013•蒙山县一模)如图,直线
(2013•蒙山县一模)如图,直线