题目内容
【题目】已知：如图，等腰△ABC中，AB=AC，点D为△ABC的BC边上一点，连接AD，将线段AD旋转至AE，使得∠DAE=∠BAC，连接CE．
（1）求证：△ACE≌△ABD；
（2）若∠BAC=∠DAE=90°，EC=3，CD=1，求四边形AECD的面积．
【答案】（1）见解析；（2）4
【解析】
（1）求出∠CAE=∠BAD，AE=AD，根据SAS推出全等即可；
（2）根据全等求出BD，求出BC，根据题意求得SAECD=S⊿ABC进而进行分析求解即可．
解：证明
(1) ∵∠DAE=∠BAC，
∴∠DAE-∠DAC= ∠BAC-∠DAC，
∴∠CAE= ∠BAD，
∵ 在⊿CAE和⊿BAD中，
AB=AC ∠CAE= ∠BAD AD=AE，
∴⊿ACE≌⊿ABD（SAS）.
(2) ∵ ⊿ACE≌⊿ABD
∴S⊿ACE =S⊿ABD ， EC=BD=3，
∴SAECD=S⊿ABC
又BC=BD+DC=4,∠BAC=900,AB=AC,
∴SAECD=S⊿ABC=
AB×AC=AB2=
=4,
新思维假期作业暑假吉林大学出版社系列答案
【题目】某年级共有300名学生，为了解该年级学生A，B两门课程的学习情况，从中随机抽取60名学生进行测试，获得了他们的成绩(百分制)、并对数据(成绩)进行整理、描述和分析，下面给出了部分信息．
a．A课程成绩的频数分布直方图如下(数据分成6组：40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x＜100)；
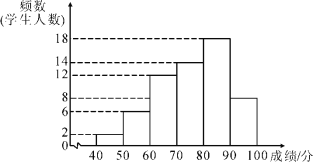
b．A课程成绩在70≤x＜80这一组的是：
70 71 71 71 76 76 77 78 78.5 78.5 79 79 79 79.5
c．A，B两门课程成绩的平均数、中位数、众数如下：
课程 | 平均数 | 中位数 | 众数 |
A | 75.8 | m | 84.5 |
B | 72.2 | 70 | 83 |
根据以上信息，回答下列问题：
(1)写出表中m的值；
(2)在此次测试中，某学生的A课程成绩为76分，B课程成绩为71分，这名学生成绩排名更靠前的课程是______(填“A”或“B”)，理由是________________________________；
(3)假设该年级学生都参加此次测试，估计A课程成绩超过75.8分的人数．
