题目内容
如图,已知一次函数y1=-x+b的图象与y轴交于点A(0,4), y2=kx-2的图象与x轴交于点B(1,0).那么使y1>y2成立的自变量x的取值范围是 .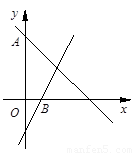
【答案】
x<2
【解析】
试题分析:先根据待定系数法分别求得两个函数的解析式,再求得两个函数图象交点的横坐标,最后观察图象得到y1的图象在y2=的图象上方的部分对应的自变量x的取值范围即可得到结果.
由一次函数y1=-x+b的图象与y轴交于点A(0,4)可得b=4
由一次函数y2=kx-2的图象与x轴交于点B(1,0)可得k=2
由-x+4=2x-2解得x=2
则由图象可得使y1>y2成立的自变量x的取值范围是x<2.
考点:一次函数的图象
点评:解题的关键是熟练掌握图象在上方的部分对应的函数值较大,在下方的部分对应的函数值较小.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
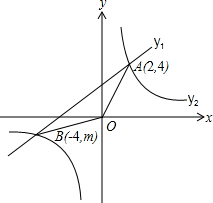 B(-4,m)两点.
B(-4,m)两点. 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=- (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数 如图,已知一次函数y=kx+b的图象交反比例函数
如图,已知一次函数y=kx+b的图象交反比例函数