��Ŀ����
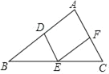
����Ŀ����ͼ1����A��B��C��DΪֱ��l�ϴ�����˳�ε�4���㣮

(1) ��ֱ��l����A��B��C��DΪ�˵���߶ι��� ����
����AC=5cm��BD=6cm��BC=1cm����PΪֱ��l��һ�㣬��PA+PD����СֵΪ cm��(2)����A��ֱ��l�������˶����߶�BD��ֱ��l�������˶���M��N�ֱ�ΪAC��BD���е㣨��ͼ2������ָ���ڴ˹������߶�AD��BC��MN�к�������ϵ��˵�����ɣ�
(3)��C��AD��һ�����ȷֵ㣬DC��AC����AD=9cm��E��F����ͬʱ��C��D�������ֱ���2cm/s��1cm/s���ٶ���ֱ��l�����˶���QΪEF���е㣬���˶�ʱ��Ϊt����AQ+AE+AF=![]() ADʱ����ֱ��д��t��ֵ��
ADʱ����ֱ��д��t��ֵ��
���𰸡�(1) ��6������10��(2)![]() ��֤����������(3)
��֤����������(3) ![]() .
.
��������
��1���������߶εĶ�����ͼ�μ��ɵó��𰸣���PA+PD��С����PΪAD���е㣬���AD�ij����ɣ�
(2) ����M��N�ֱ�ΪAC��BD���е㣬�õ�![]() ��
��![]() ������
������![]() ���뻯�ɣ�
���뻯�ɣ�
(3) ����C��AD��һ�����ȷֵ㣬DC��AC����AD=9cm���õ�![]() ��
��![]() �����ɵõ�
�����ɵõ�![]() ��
��![]() ��
��![]() ������AQ+AE+AF=
������AQ+AE+AF=![]() AD������������t.
AD������������t.
�⣺(1) ���߶��У�AB��AC��AD��BC��BD��CD����6����
�ڡ�BD=6��BC=1��
��CD=BD-BC=6-1=5��
��PA+PD��ֵ��Сʱ��PΪAD���е㣬
��![]() ��
��
(2)![]() .
.
��ͼ2ʾ��
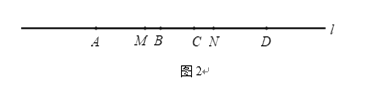
��M��N�ֱ�ΪAC��BD���е㣬
��![]() ��
��![]()
��![]()
![]()
![]()
![]()
![]() ��
��
(3)��ͼʾ��

��C��AD��һ�����ȷֵ㣬DC��AC����AD=9cm��
��![]() ��
��![]() ��
��
����E��F����ͬʱ��C��D�������ٶ���2cm/s��1cm/s��QΪEF���е㣬�˶�ʱ��Ϊt��
����![]() ��
��![]() ��
��![]()
��AQ+AE+AF=![]() ADʱ��
ADʱ��
����![]()
���ǣ�![]()
��֮�ã�![]() .
.

����Ŀ��ijͬѧ��ȡ20��ѧ��ͳ��ij�µ��ñ����������������±���
�ñ�����֧�� | 4 | 5 | 6 | 8 | 9 |
ѧ���� | 4 | 4 | 7 | 3 | 2 |
�������20��ѧ������µ��ñ�����������������˵����ȷ����( ) ��
A. ������7֧ B. ��λ����6֧ C. ƽ������5֧ D. ����Ϊ0