题目内容
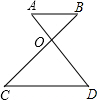 (2012•虹口区一模)如图,若AD=3AO,则当CO:BO的值为
(2012•虹口区一模)如图,若AD=3AO,则当CO:BO的值为2
2
时,有AB∥CD成立.分析:先由AD=3AO,得出DO:AO=2,则当CO:BO的值为2时,根据两边对应成比例且夹角相等的两三角形相似证明△COD∽△BOA,由相似三角形对应边成比例得出∠C=∠B,然后根据内错角相等,两直线平行得出AB∥CD.
解答:解:如图,当CO:BO的值为2时,有AB∥CD成立.理由如下:
∵AD=3AO,AD=AO+DO,
∴DO=2AO,即DO:AO=2.
在△COD与△BOA中,
∵DO:AO=CO:BO=2,∠COD=∠BOA,
∴△COD∽△BOA,
∴∠C=∠B,
∴AB∥CD.
故答案为2.
∵AD=3AO,AD=AO+DO,
∴DO=2AO,即DO:AO=2.
在△COD与△BOA中,
∵DO:AO=CO:BO=2,∠COD=∠BOA,
∴△COD∽△BOA,
∴∠C=∠B,
∴AB∥CD.
故答案为2.
点评:本题考查了相似三角形的判定与性质,平行线的判定,难度适中,根据条件证明△COD∽△BOA,是解题的关键.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 (2012•虹口区一模)如图,分别以下列选项作为一个已知条件,其中不一定能得到△AOB∽△COD的是( )
(2012•虹口区一模)如图,分别以下列选项作为一个已知条件,其中不一定能得到△AOB∽△COD的是( )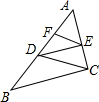 (2012•虹口区一模)如图,已知EF∥CD,DE∥BC,下列结论中不一定正确的是( )
(2012•虹口区一模)如图,已知EF∥CD,DE∥BC,下列结论中不一定正确的是( )