题目内容
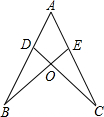
 如图所示,点E在AC上,AB=AD,BC=DC,则图中全等的三角形有
如图所示,点E在AC上,AB=AD,BC=DC,则图中全等的三角形有
- A.1对
- B.2对
- C.3对
- D.4对
C
分析:由AB=AD,BC=DC,AC为公共边可以证明△ABC≌△ADC,再由全等三角形的性质可得∠BAC=∠DAC,∠BCA=∠DCA,进而可推得△ABE≌△ADE,△CBE≌△CDE.
解答:∵AB=AD,BC=DC,AC为公共边,
∴△ABC≌△ADC.
∴∠BAC=∠DAC,∠BCA=∠DCA,
∴△ABE≌△ADE,
△CBE≌△CDE.
故选C.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS;还利用了全等三角形的性质进行解题.做题时要按判定全等的方法逐个验证,从已知开始结合全等的判定方法由易到难逐个找寻.
分析:由AB=AD,BC=DC,AC为公共边可以证明△ABC≌△ADC,再由全等三角形的性质可得∠BAC=∠DAC,∠BCA=∠DCA,进而可推得△ABE≌△ADE,△CBE≌△CDE.
解答:∵AB=AD,BC=DC,AC为公共边,
∴△ABC≌△ADC.
∴∠BAC=∠DAC,∠BCA=∠DCA,
∴△ABE≌△ADE,
△CBE≌△CDE.
故选C.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS;还利用了全等三角形的性质进行解题.做题时要按判定全等的方法逐个验证,从已知开始结合全等的判定方法由易到难逐个找寻.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 22、如图所示,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=EB,求∠A的度数.
22、如图所示,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=EB,求∠A的度数.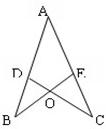 15、如图所示,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若∠B=20°,则∠C=
15、如图所示,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若∠B=20°,则∠C=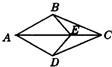
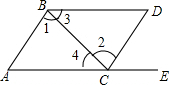 如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )
如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )