题目内容
【题目】在四边形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点
的中点
情景引入:
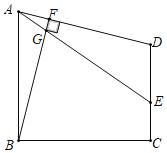
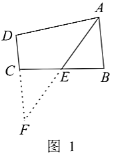
(1)如图1,若![]() 是
是![]() 的平分线,试判断
的平分线,试判断![]() ,
,![]() ,DC之间的等量关系.
,DC之间的等量关系.
解决此问题可以用如下方法:延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,证明
,证明![]() 得到
得到![]() ,从而把
,从而把![]() ,
,![]() ,
,![]() 转化在一个三角形中即可判断
转化在一个三角形中即可判断![]() ,
,![]() ,
,![]() 之间的等量关系为
之间的等量关系为![]() ,试证明该结论;
,试证明该结论;
问题探究:
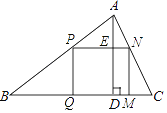
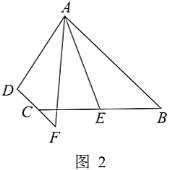
(2)如图2,点![]() 是
是![]() 的延长线上一点,连
的延长线上一点,连![]() ,若
,若![]() 恰好是
恰好是![]() 的平分线,试探究
的平分线,试探究![]() ,
,![]() ,
,![]() 之间的等量关系,并证明你的结论.
之间的等量关系,并证明你的结论.
【答案】(1)见解析;(2)AB=AF+CF,理由见解析.
【解析】
(1)由“AAS”可证△CEF≌△BEA,可得AB=CF,即可得结论;
(2)延长AE交DF的延长线于点G,由“AAS”可证△AEB≌△GEC,可得AB=CG,即可得结论.
解:(1)AD=AB+DC
理由如下:∵AE是∠BAD的平分线
∴∠DAE=∠BAE
∵AB∥CD
∴∠F=∠BAE
∴∠DAF=∠F
∴AD=DF,
∵点E是BC的中点
∴CE=BE,且∠F=∠BAE,∠AEB=∠CEF
∴△CEF≌△BEA(AAS)
∴AB=CF
∴AD=CD+CF=CD+AB
(2)AB=AF+CF
理由如下:如图②,延长AE交DF的延长线于点G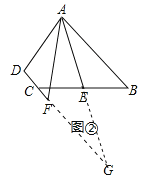
∵E是BC的中点,
∴CE=BE,
∵AB∥DC,
∴∠BAE=∠G.且BE=CE,∠AEB=∠GEC
∴△AEB≌△GEC(AAS)
∴AB=GC
∵AE是∠BAF的平分线
∴∠BAG=∠FAG,
∵∠BAG=∠G,
∴∠FAG=∠G,
∴FA=FG,
∵CG=CF+FG,
∴AB=AF+CF

练习册系列答案
相关题目