题目内容
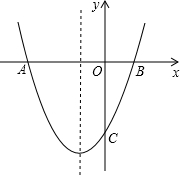 (2011•利川市一模)如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0).
(2011•利川市一模)如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0).(1)求这条抛物线的函数表达式;
(2)已知在抛物线的对称轴上存在一点P,使得PB+PC的值最小,请求出点P的坐标;
(3)若点D是线段OC上的一个动点(不与点O、点C重合).过点D作DE∥PC交x轴于点E.连接PD、PE.设CD的长为m,△PDE的面积为S.求S与m之间的函数关系式.试说明S是否存在最大值?若存在,请求出最大值;若不存在,请说明理由.
分析:(1)把A、B的坐标代入二次函数的解析式,即可得到方程组求得a,b的值,从而得到函数的解析式;
(2)求出C关于对称轴的对称点C′坐标,然后利用待定系数法求得直线BC′的解析式,与对称轴的交点就是P;
(3)求得DE的解析式,进而得到PF、OE的长度,根据S=
PF•OE即可求得函数的解析式.
(2)求出C关于对称轴的对称点C′坐标,然后利用待定系数法求得直线BC′的解析式,与对称轴的交点就是P;
(3)求得DE的解析式,进而得到PF、OE的长度,根据S=
| 1 |
| 2 |
解答: 解:(1)根据题意得:
解:(1)根据题意得:
,
解得:
,
则抛物线的函数表达式是:y=
x2+
x-4;
(2)在:y=
x2+
x-4,中令x=0,解得y=-4,则C的坐标是(0,-4).
二次函数的解析式是:x=-
=-2,
C关于x=-2的对称点C′的坐标是(-4,-4).
设直线BC′的解析式是y=kx+b,
则
,
解得:
,
在直线的解析式是:y=
x-
,令x=-2,解得y=-
,
则P的坐标是:(-2,-
);
(3)设D的坐标是(0,c),
设直线PC的解析式是y=ex+f,则
,
解得:
,
则直线的解析式是:y=-
x-4,
因为CD=m,则D的坐标是(m-4,0),则直线DE的解析式是:y=-
x+(m-4).
令x=-2,解得:y=m-
,故F的坐标是(-2,m-
),则PF=m,
令y=0,解得:x=
m-6.即OE=6-
m.
E的面积为S=
PF•OE=
m(6-
m),
即S=-
m2+3m(0<m<4).
当x=
=2时,有最大值是:3.
 解:(1)根据题意得:
解:(1)根据题意得:
|
解得:
|
则抛物线的函数表达式是:y=
| 1 |
| 3 |
| 4 |
| 3 |
(2)在:y=
| 1 |
| 3 |
| 4 |
| 3 |
二次函数的解析式是:x=-
| ||
|
C关于x=-2的对称点C′的坐标是(-4,-4).
设直线BC′的解析式是y=kx+b,
则
|
解得:
|
在直线的解析式是:y=
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
则P的坐标是:(-2,-
| 8 |
| 3 |
(3)设D的坐标是(0,c),
设直线PC的解析式是y=ex+f,则
|
解得:
|
则直线的解析式是:y=-
| 2 |
| 3 |
因为CD=m,则D的坐标是(m-4,0),则直线DE的解析式是:y=-
| 2 |
| 3 |
令x=-2,解得:y=m-
| 8 |
| 3 |
| 8 |
| 3 |
令y=0,解得:x=
| 3 |
| 2 |
| 3 |
| 2 |
E的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
即S=-
| 3 |
| 4 |
当x=
| 3 | ||
|
点评:本题考查了对称点的性质,待定系数法求函数的解析式,直线平行的条件的综合应用,求得DE的解析式是关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
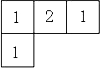 (2011•利川市一模)如图所示,是几个相同小正方体所搭成几何体的俯视图,小正方形内的数字表示在该位置的小正方体的个数.则这个几何体的主视图是( )
(2011•利川市一模)如图所示,是几个相同小正方体所搭成几何体的俯视图,小正方形内的数字表示在该位置的小正方体的个数.则这个几何体的主视图是( ) (2011•利川市一模)如图,反映的是九(3)班学生某次数学考试成绩不及格、及格、优分的人数分布直方图和扇形统计图(部分),则下列说法中不正确的是( )
(2011•利川市一模)如图,反映的是九(3)班学生某次数学考试成绩不及格、及格、优分的人数分布直方图和扇形统计图(部分),则下列说法中不正确的是( )