Question

【题目】已知：如图，抛物线y=-x2+bx+c与x轴负半轴交于点A，与x轴正半轴交于点B，与y轴正半轴交于点C，OA=3，OB=1，点M为点A关于y轴的对称点.

（1）求抛物线的解析式；

（2）点P为第三象限抛物线上一点，连接PM、PA，设点P的横坐标为t，△PAM的面积为S，求S与t的函数关系式；

（3）在（2）的条件下，PM交y轴于点N，过点A作PM的垂线交过点C与x轴平行的直线于点G，若ON∶CG=1∶4，求点P的坐标.

Answer 1

【答案】（1）；（2）；（3）P（， ）

【解析】试题分析： 把点点代入函数解析式，求得函数解析式即可.

点的横坐标为，纵坐标为，利用三角形的面积公式即可表示出的面积.

设 直线的斜率

直线的斜率 直线垂直, 解得： 直线的方程是： 和抛物线的方程联立，即可求出点的坐标.

试题解析：

把 代入,

解得：

抛物线的解析式为

由题意可知,点,点

如图所示,

点在第三象限，

如图所示，

设

直线的斜率

直线的斜率

直线垂直,

解得：

直线的方程是：

联立方程：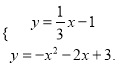

解得：

点的坐标为：