题目内容
【题目】如图,在平面直角坐标系中,长方形OABC的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.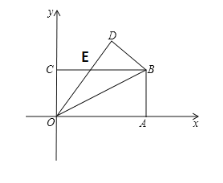
(1)求点E的坐标;
(2)点M是OB上任意一点,点N是OA上任意一点,是否存在点M、N,使得AM+MN最小?若存在,求出其最小值,若不存在,请说明理由.
【答案】(1)E(3,4);(2)存在,![]()
【解析】
(1)根据翻折特点可得∠DOB=∠AOB,由平行性质可得∠OBC=∠DOB,故EO=EB,设OE=x,则DE=8-x,根据勾股定理得,DB2+DE2=BE2,即16+(8-x)2=x2,可进一步求出E的坐标;
(2)过点D作OA的垂线交OB于M,交OA于N,此时的M,N是AM+MN的最小值的位置,求出DN就是AM+MN的最小值,结合(1),根据面积有DE×BD=BE×DG,故DG=![]() ,得GN=OC=4,可求出DN=DG+GN.
,得GN=OC=4,可求出DN=DG+GN.
(1)∵将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
∴∠DOB=∠AOB,
∵BC∥OA,
∴∠OBC=∠AOB,
∴∠OBC=∠DOB,
∴EO=EB,
∵长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),
设OE=x,则DE=8-x,
在Rt△BDE中,BD=4,根据勾股定理得,DB2+DE2=BE2,
∴16+(8-x)2=x2,
∴x=5,
∴BE=5,
∴CE=3,
∴E(3,4);
(2)如图,

过点D作OA的垂线交OB于M,交OA于N,此时的M,N是AM+MN的最小值的位置,求出DN就是AM+MN的最小值,
由(1)得,DE=3,BE=5,BD=4,
∴根据面积有DE×BD=BE×DG,
∴DG=![]() 由题意有,GN=OC=4,
由题意有,GN=OC=4,
∴DN=DG+GN=![]()
即:AM+MN的最小值是![]() .
.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】在一个不透明的袋子中装有仅颜色不同的![]() 个小球,其中红球
个小球,其中红球![]() 个,白球
个,白球![]() 个.
个.
(1)先从袋子中取出![]() 个红球(
个红球(![]() 且
且![]() 为正整数),再从袋子中随机摸
为正整数),再从袋子中随机摸![]() 个小球,将“摸出白球”记为事件A,请完成下面表格:
个小球,将“摸出白球”记为事件A,请完成下面表格:
事件 | 必然事件 | 随机事件 |
|
(2)先从袋子中取出![]() 个红球,再放入
个红球,再放入![]() 个一样的白球并掘匀,随机摸出
个一样的白球并掘匀,随机摸出![]() 个白球的频率在
个白球的频率在![]() 附近摆动,求
附近摆动,求![]() 的值.
的值.




