题目内容
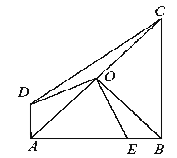
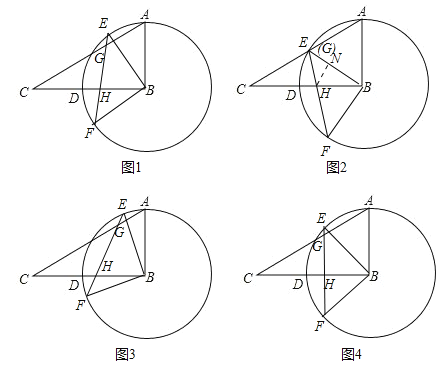
【题目】在直角三角形ABC中,∠ABC=90°,∠C=30°,AB=4,以B为圆心,BA为半径作⊙B交BC于点D,旋转∠ABD交⊙B于点E、F,连接EF交AC、BC边于点G、H.
(1)若BE⊥AC,求tan∠CGH的值;
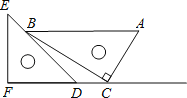
(2)若AG=4,求△BEF与△ABC重叠部分的面积;
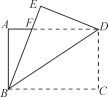
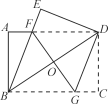
(3)△BHE是等腰三角形时,∠ABD逆时针旋转的度数是_____.

【答案】(1)1;(2)4![]() -4;(3)22.5°或45°.
-4;(3)22.5°或45°.
【解析】试题分析:(1)先判断出AC∥BF,进而得出∠CGH=F=45°,即可得出结论;
(2)易知当AG=4时,点G为AC中点,与点E重合,如图2,过点H作HN⊥BE于N,△BEF与△ABC重叠部分的面积就是△EBH的面积,只需运用三角函数求出HN,即可解决问题;
(3)只需将△BHE的三个内角分别作为等腰三角形的顶角进行分类讨论,就可解决问题.
试题解析:解:(1)如图1.∵BE⊥AC,BE⊥BF,∴AC∥BF,∴∠CGH=∠F=45°,∴tan∠CGH=tan45°=1;
(2)∵∠ABC=90°,∠C=30°,AB=4,∴AC=8.∵AG=4,∴点G是AC的中点,此时E与G重合,△ABE是等边三角形,如图2.过点H作于HN⊥BE于N,∠BEF=45°,BE=BF,∴∠EHN=90°﹣45°=45°=∠BEF,∴EN=HN.设HN=x,则EN=x,NB=4﹣x.在Rt△HNB中,由tan∠NBH=![]() ,得:
,得:![]() ,解得:
,解得:![]() ,∴S△EBH=
,∴S△EBH=![]() ,即△BEF与△ABC重叠部分的面积为
,即△BEF与△ABC重叠部分的面积为![]() ;
;
(3)①若∠HEB是等腰△BHE的顶角,如图3,则有∠EBH=∠EHB=![]() =67.5°,∴∠ABE=90°﹣67.5°=22.5°.
=67.5°,∴∠ABE=90°﹣67.5°=22.5°.
②若∠EHB是等腰△BHE的顶角,如图4,则有∠EBH=∠HEB=45°,∴∠ABE=90°﹣45°=45°.
③若∠EBH是等腰△BHE的顶角,则∠EBH=180°﹣45°﹣45°=90°,此时点E与点A重合,没有旋转,故舍去.
综上所述:△BHE是等腰三角形时的旋转角的度数为22.5°或45°.

 优学名师名题系列答案
优学名师名题系列答案