题目内容
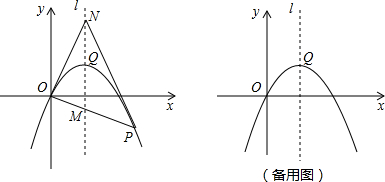
(2013•晋江市质检)如图,抛物线y=a(x-4)2+4(a≠0)经过原点O(0,0),点P是抛物线上的一个动点,OP交其对称轴l于点M,且点M、N关于顶点Q对称,连结PN、ON.
(1)求a的值;
(2)当点P在对称轴l右侧的抛物线上运动时,试解答如下问题:
①是否存在点P,使得ON⊥OP?若存在,试求出点P的坐标;否则请说明理由;
②试说明:△OPN的内心必在对称轴l上.
(1)求a的值;
(2)当点P在对称轴l右侧的抛物线上运动时,试解答如下问题:
①是否存在点P,使得ON⊥OP?若存在,试求出点P的坐标;否则请说明理由;
②试说明:△OPN的内心必在对称轴l上.

分析:(1)把原点的坐标代入抛物线解析式,列出关于a的方程0=a(0-4)2+4,通过解方程0=a(0-4)2+4来求a的值;
(2)①根据题意,可点P(x0, -
+2x0),则易求得AN=OD=4,OB=
-2x0,BP=x0,OA=x0.
如图1所示,作NA⊥y轴于点A,PB⊥y轴于点B,构建相似三角形:△ANO∽△BOP.由该相似三角形的对应边成比例求得x0=4+4
,即点P的坐标(4+4
, -4);
②欲证明△OPN的内心必在对称轴l上,只需证明直线l平分∠ONP即可.
(2)①根据题意,可点P(x0, -
| 1 |
| 4 |
| x | 2 0 |
| 1 |
| 4 |
| x | 2 0 |
如图1所示,作NA⊥y轴于点A,PB⊥y轴于点B,构建相似三角形:△ANO∽△BOP.由该相似三角形的对应边成比例求得x0=4+4
| 2 |
| 2 |
②欲证明△OPN的内心必在对称轴l上,只需证明直线l平分∠ONP即可.
解答: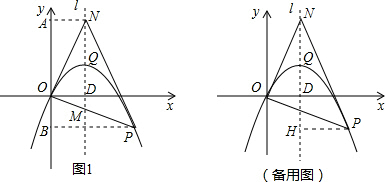 解:(1)把点O(0,0)代入y=a(x-4)2+4,得:0=a(0-4)2+4,解得:a=-
解:(1)把点O(0,0)代入y=a(x-4)2+4,得:0=a(0-4)2+4,解得:a=-
.
(2)由(1)得:a=-
,
∴抛物线的解析式是y=-
(x-4)2+4,即y=-
x2+2x.
∵点P是抛物线上的点,
∴设点P(x0, -
+2x0)
则直线OP的解析式为:y=
x=(-
x0+2)x.
∴M(4,-x0+8),
由y=-
(x-4)2+4可得顶点Q(4,4),又点M、N关于顶点Q对称
∴N(4,x0)
∴AN=OD=4,OB=
-2x0,BP=x0,OA=x0
若ON⊥OP,则∠NOP=90°,显然点P在第四象限,
如图1所示,作NA⊥y轴于点A,PB⊥y轴于点B.
∴∠OPB+∠POB=90°,∠OPB=∠AON(同角的余角相等).
∴△ANO∽△BOP.
∴
=
,即
=
,即
-8x0-16=0,
解得:x0=4±4
,
又x0>4
∴x0=4+4
∴点P(4+4
, -4)
故当点P在对称轴l右侧的抛物线上运动时,存在点P的坐标(4+4
, -4),使得ON⊥OP.
②如备用图,作PH⊥l于点H.
由点P(x0, -
+2x0)、N(4,x0),可得:PH=x0-4,NH=x0-(-
+2x0)=
-x0,
在Rt△PHN中,tan∠PNH=
=
=
,
在Rt△ODN中,tan∠OND=
=
,
∴tan∠PNH=tan∠OND
∴∠PNH=∠OND,即直线l平分∠ONP,
∴△OPN的内心必在对称轴l上.
 解:(1)把点O(0,0)代入y=a(x-4)2+4,得:0=a(0-4)2+4,解得:a=-
解:(1)把点O(0,0)代入y=a(x-4)2+4,得:0=a(0-4)2+4,解得:a=-| 1 |
| 4 |
(2)由(1)得:a=-
| 1 |
| 4 |
∴抛物线的解析式是y=-
| 1 |
| 4 |
| 1 |
| 4 |
∵点P是抛物线上的点,
∴设点P(x0, -
| 1 |
| 4 |
| x | 2 0 |
则直线OP的解析式为:y=
-
| ||||
| x0 |
| 1 |
| 4 |
∴M(4,-x0+8),
由y=-
| 1 |
| 4 |
∴N(4,x0)
∴AN=OD=4,OB=
| 1 |
| 4 |
| x | 2 0 |
若ON⊥OP,则∠NOP=90°,显然点P在第四象限,
如图1所示,作NA⊥y轴于点A,PB⊥y轴于点B.
∴∠OPB+∠POB=90°,∠OPB=∠AON(同角的余角相等).
∴△ANO∽△BOP.
∴
| OB |
| AN |
| BP |
| OA |
| ||||
| 4 |
| x0 |
| x0 |
| x | 2 0 |
解得:x0=4±4
| 2 |
又x0>4
∴x0=4+4
| 2 |
∴点P(4+4
| 2 |
故当点P在对称轴l右侧的抛物线上运动时,存在点P的坐标(4+4
| 2 |
②如备用图,作PH⊥l于点H.
由点P(x0, -
| 1 |
| 4 |
| x | 2 0 |
| 1 |
| 4 |
| x | 2 0 |
| 1 |
| 4 |
| x | 2 0 |
在Rt△PHN中,tan∠PNH=
| PH |
| NH |
| x0-4 | ||||
|
| 4 |
| x0 |
在Rt△ODN中,tan∠OND=
| OD |
| DN |
| 4 |
| x0 |
∴tan∠PNH=tan∠OND
∴∠PNH=∠OND,即直线l平分∠ONP,
∴△OPN的内心必在对称轴l上.
点评:本题综合考查了待定系数法求二次函数解析式,相似三角形的判定与性质以及三角形内心的定义.在解答(1)①时,也可以由△ODM∽△PBO求得DM=x0-8,即M(4,-x0+8).

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 (2013•晋江市质检)如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点AD=BC=8,EF=7.6,则△PEF的周长是
(2013•晋江市质检)如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点AD=BC=8,EF=7.6,则△PEF的周长是