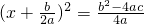题目内容
不解方程,判别下列方程的根的情况:(1)2x2+3x-4=0;
(2)16y2+9=24y;
(3)
| 3 |
| 2 |
(4)3t2-3
| 6 |
(5)5(x2+1)-7x=0.
分析:把各式化成一元二次方程的一般式,求出根的判别式△=b2-4ac,然后判断是否有实数根.
解答:解:(1)2x2+3x-4=0;
△=b2-4ac=9+32=41>0,
故方程有两不相等的实数根,
(2)16y2+9=24y;
△=b2-4ac=576-4×16×9=0,
故方程有两相等的实数根,
(3)
x2-
x+2=0;
△=b2-4ac=2-8
<0,
故方程没有实数根,
(4)3t2-3
t+2=0;
△=b2-4ac=54-4×3×2=30>0,
故方程有两不相等的实数根,
(5)5(x2+1)-7x=0,
△=b2-4ac=49-4×5×5=-51<0,
故方程没有实数根.
△=b2-4ac=9+32=41>0,
故方程有两不相等的实数根,
(2)16y2+9=24y;
△=b2-4ac=576-4×16×9=0,
故方程有两相等的实数根,
(3)
| 3 |
| 2 |
△=b2-4ac=2-8
| 3 |
故方程没有实数根,
(4)3t2-3
| 6 |
△=b2-4ac=54-4×3×2=30>0,
故方程有两不相等的实数根,
(5)5(x2+1)-7x=0,
△=b2-4ac=49-4×5×5=-51<0,
故方程没有实数根.
点评:本题主要考查根的判别式的知识点,当△=b2-4ac>0,方程有两不等的实数根,当△=b2-4ac=0,方程有两相等的实数根,△=b2-4ac<0,方程没有实数根.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
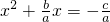
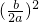 ,得
,得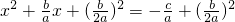 ,即
,即