题目内容
（1997•陕西）如图，圆内接正六边形ABCDEF中，AC，BF相交于点O，则S△ABO：S△AFO=1：2
1：2
．分析：先根据正六边形的性质判断出∠1=∠2=∠3=30°，∠CAF=90°，再求出△ABO与△AOF的高之比即可．
解答：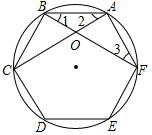
解：∵六边形ABCDEF是正六边形，
∴
=
=
=
=
=
，
∴∠1=∠2=∠3=30°，∠CAF=90°，
∴AO=BO，在Rt△AOF中，AO=
OF，
∴BO=
OF，
∵△ABO和△AOF等高，底边BO：FO=1：2，
即S△ABO：S△AFO=1：2．
故答案为：1：2．
解：∵六边形ABCDEF是正六边形，∴
 |
| AB |
|
| BC |
|
| AF |
|
| EF |
|
| DE |
|
| CD |
∴∠1=∠2=∠3=30°，∠CAF=90°，
∴AO=BO，在Rt△AOF中，AO=
| 1 |
| 2 |
∴BO=
| 1 |
| 2 |
∵△ABO和△AOF等高，底边BO：FO=1：2，
即S△ABO：S△AFO=1：2．
故答案为：1：2．
点评：本题考查了正六边形及等腰三角形的性质、圆周角定理，综合性较强，但难度适中．
练习册系列答案
培优口算题卡系列答案
相关题目
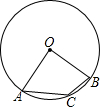（1997•陕西）如图，已知在⊙O中，点A，B，C均在圆上，∠AOB=80°，则∠ACB等于（ ）
（1997•陕西）如图，已知在△ABC中，AD是BC边上的中线，则下列结论中正确的是（ ）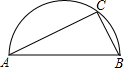
（1997•陕西）如图，已知△ABC内接于半径为r的半圆内，直径AB为其一边，设AC+BC=S，则有（ ）
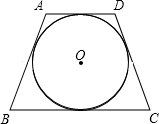（1997•陕西）如图，四边形ABCD是⊙O的外切等腰梯形，其周长为20，则梯形ABCD的中位线长为
（1997•陕西）如图，已知矩形ABCD中，AB=10，BC=12，E为DC的中点，AF⊥BE于点F，则AF=