题目内容
【题目】如图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
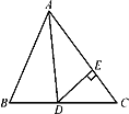
【答案】(1)∠ADBD=84°.
(2)∠ADE=60°.
【解析】试题分析:(1)已知∠B,∠C的度数,可求出三角形ABC中![]() BAC的度数,AD又是
BAC的度数,AD又是![]() BAC的角平分线,可以求得
BAC的角平分线,可以求得![]() BAD的值,从而在三角形ABD中即可求得∠ADB的度数。(2)由(1)可求得
BAD的值,从而在三角形ABD中即可求得∠ADB的度数。(2)由(1)可求得![]() CAD=
CAD=![]() BAD,若DE⊥AC,则在直角三角形中可以求得∠ADE的度数。
BAD,若DE⊥AC,则在直角三角形中可以求得∠ADE的度数。
试题解析:(1)∵在△ABC中,∠B=66°,∠C=54°,
∴∠BAC=180°-∠B-∠C=60°.
∵AD是∠BAC的平分线,
∴∠BAD=![]() ∠BAC=30°.
∠BAC=30°.
在△ABD中,∠B=66°,∠BAD=30°,
∴∠ADB=180°-∠B-∠BAD=84°.
(2)∵∠CAD=![]() ∠BAC=30°,DE⊥AC,
∠BAC=30°,DE⊥AC,
∴∠ADE=90°-∠EAD=60°.

练习册系列答案
相关题目