题目内容
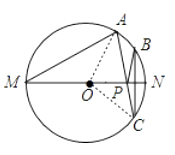
【题目】如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为 . 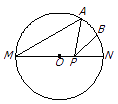
【答案】![]()
【解析】作点B关于MN的对称点C,连接AC交NM于点P,则P点就是所作的点;
∴PB=PC,
∴PA+PB=PA+PC=AC,
即此时PA+PB最小,
连接OA,OC,
∵∠AMN=30°,
∴∠AON=60°,
∴弧AN的度数为60°,
又∵B为弧AN的中点,
∴弧BN的度数为30°,
又∵点B关于MN的对称点为C,
∴弧CN的度数为30°,
∴∠AOC=90°,
又∵MN是⊙O的直径,MN=2,
∴OA=OC=1,
∴AC=![]() =
=![]() .
.
所以答案是:![]() .
.
【考点精析】利用勾股定理的概念和圆心角、弧、弦的关系对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目