题目内容
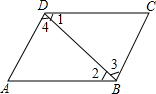 如图所示,下列推理正确的个数有( )
如图所示,下列推理正确的个数有( )①若∠1=∠2,则AB∥CD
②若AD∥BC,则∠3+∠A=180°
③若∠C+∠CDA=180°,则AD∥BC
④若AB∥CD,则∠3=∠4.
分析:根据平行线的判定(内错角相等,两直线平行,同位角相等,两直线平行,同旁内角互补,两直线平行)和平行线的性质(两直线平行,内错角相等,两直线平行,同位角相等,两直线平行,同旁内角互补)判断即可.
解答:解:∵∠1=∠2,
∴AB∥DC,∴①正确;
∵AD∥BC,
∴∠CBA+∠A=180°,∠3+∠A<180°,∴②错误;
∵∠C+∠CDA=180°,
∴AD∥BC,∴③正确;
由AD∥BC才能推出∠3=∠4,而由AB∥CD不能推出∠3=∠4,∴④错误;
正确的个数有2个,
故选C,
∴AB∥DC,∴①正确;
∵AD∥BC,
∴∠CBA+∠A=180°,∠3+∠A<180°,∴②错误;
∵∠C+∠CDA=180°,
∴AD∥BC,∴③正确;
由AD∥BC才能推出∠3=∠4,而由AB∥CD不能推出∠3=∠4,∴④错误;
正确的个数有2个,
故选C,
点评:本题考查了对平行线的性质和判定的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
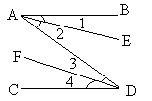
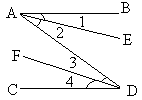
 如图所示,下列推理正确的是( )
如图所示,下列推理正确的是( )