题目内容
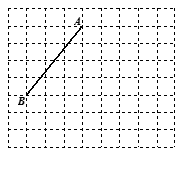
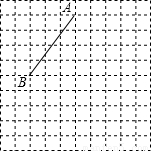
如图线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A按逆时针方向旋 转90°得到线段AC.
转90°得到线段AC.(1)请你用尺规在所给的网格中画出线段AC及点B经过的路径;
(2)若将此网格放在一平面直角坐标系中,已知点A的坐标为(1,3),点B的坐标为(-2,-1),则点C的坐标为
(3)线段AB在旋转到线段AC的过程中,线段AB扫过的区域的面积为
(4)若有一张与(3)中所说的区域形状相同的纸片,将它围成一个几何体的侧面,则该几何体底面圆的半径长为
分析:(1)线段AB绕点A按逆时针方向旋转90°得到线段AC.线段AC及点B经过的路径是一段弧,根据弧长公式计算路径;
(2)根据点A的坐标为(1,3),点B的坐标为(-2,-1),可建立直角坐标系,从直角坐标系中读出点C的坐标为(5,0);
(3)线段AB在旋转到线段AC的过程中,线段AB扫过的区域的面积为一个扇形,根据扇形公式计算;
(4)将它围成一个几何体即圆锥的侧面,则该几何体底面圆的周长就等于弧长,利用此等量关键可计算出半径.
(2)根据点A的坐标为(1,3),点B的坐标为(-2,-1),可建立直角坐标系,从直角坐标系中读出点C的坐标为(5,0);
(3)线段AB在旋转到线段AC的过程中,线段AB扫过的区域的面积为一个扇形,根据扇形公式计算;
(4)将它围成一个几何体即圆锥的侧面,则该几何体底面圆的周长就等于弧长,利用此等量关键可计算出半径.
解答: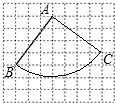 解:(1)如图,
解:(1)如图,
为点B经过的路径;
(2)(5,0);
(3)线段AB在旋转到线段AC的过程中,线段AB扫过的区域的面积为一个扇形,
根据扇形公式计算
=
π;(6分)
(4)将它围成一个几何体即圆锥的侧面,则该几何体底面圆的周长就等于弧长,
=2πr
解得r=
.(8分)
 解:(1)如图,
解:(1)如图, |
| BC |
(2)(5,0);
(3)线段AB在旋转到线段AC的过程中,线段AB扫过的区域的面积为一个扇形,
根据扇形公式计算
| 90π×25 |
| 360 |
| 25 |
| 4 |
(4)将它围成一个几何体即圆锥的侧面,则该几何体底面圆的周长就等于弧长,
| 90π×5 |
| 180 |
解得r=
| 5 |
| 4 |
点评:本题综合考查了坐标系,旋转图形,及圆的弧长公式,扇形的面积公式等,所以学生学过的知识一定要系统起来.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 答案直接填写在后面的横线上
答案直接填写在后面的横线上