题目内容
如图，在由边长为1cm的小正方形组成的网格中，画如图所示的燕尾形工件，现要求最大限度的裁剪出10个与它全等的燕尾形工件，则这个网格的长至少为（接缝不计）________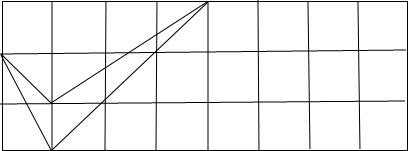
21
分析：观察图形，发现：以中间的点看，再画第二个图形的时候，需要再往右用1个格，画第三个图的时候，需要再往右用3个格，画第四个图的时候，需要再往右走1个格，以此类推，则画10个图，需要4+1+3+1+3+1+3+1+3+1=21个．
解答：∵后面画出的图形与第一个图形完全一样
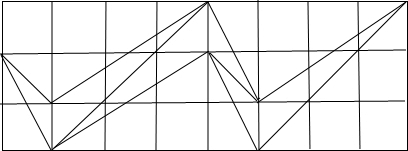
∴画第二个图形的时候，需往右用两个格，画第三个图的时候，需要再往右用三个格，画第四个图的时候，需要再往右走1个格…
∴画第10个图时，网格的长为4+（1+3+1+3+1+3+1+3+1）=21个．
点评：本题考查的是全等图形的作图，根据图形观察发现画下一个图的时候，共需要的格数，一定要找清规律．
分析：观察图形，发现：以中间的点看，再画第二个图形的时候，需要再往右用1个格，画第三个图的时候，需要再往右用3个格，画第四个图的时候，需要再往右走1个格，以此类推，则画10个图，需要4+1+3+1+3+1+3+1+3+1=21个．
解答：∵后面画出的图形与第一个图形完全一样
∴画第二个图形的时候，需往右用两个格，画第三个图的时候，需要再往右用三个格，画第四个图的时候，需要再往右走1个格…
∴画第10个图时，网格的长为4+（1+3+1+3+1+3+1+3+1）=21个．
点评：本题考查的是全等图形的作图，根据图形观察发现画下一个图的时候，共需要的格数，一定要找清规律．
练习册系列答案
相关题目
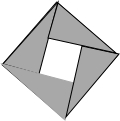2002年8月在北京召开的国际数学家大会会徽如图所示，它由四个相同的直角三角形拼成，若较长直角边为3，较短直角边为2，则图中大正方形与小正方形的面积之比是（ ）| A、3：2 | B、13：1 | C、12：1 | D、169：1 |
2002年8月在北京召开的国际数学家大会会徽如图所示，它由四个相同的直角三角形拼成，若较长直角边为3，较短直角边为2，则图中大正方形与小正方形的面积之比是