Question

（1）计算：|3-

12

|+(

6

2+ 2

)0+cos2300-4sin600
（2）先化解再求值：

x2-x

x+1

•

x2-1

x2-2x+1

，其中x满足x²-3x+2=0
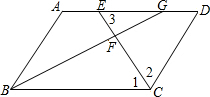
（3）如图，在平行四边形ABCD中∠BCD的平分线CE交于AD于点E，∠ABC的平分线BG交CE于点F，交AD于点G，求证：AE=DG．

Answer 1

分析：（1）根据0指数幂，二次根式的化简，绝对值，特殊角的三角函数值计算；
（2）将分子、分母因式分解，约分，再代值计算；
（3）证明△CDE和△ABG为等腰三角形，得出AG=AB，DE=CD，由平行四边形的性质可知，AB=CD，利用作差法可证AE=DG．

解答：解：（1）原式=2

3

-3+1+（

3

2

）²-4×

3

2

=2

3

-2+

3

4

-2

3

=-

5

4

；

（2）原式=

x(x-1)

x+1

•

(x+1)(x-1)

(x-1)2

=x，
解方程x²-3x+2=0得x₁=2，x₂=1（舍去），
∴当x=2时，原式=2；

（3）证明：如图，∵CE平分∠BCD，
∴∠1=∠2，
∵BC∥AD，
∴∠1=∠3，
∴∠2=∠3，
∴DE=CD，
同理可证AG=AB，
由平行四边形的性质可知AB=CD，
∴AG=DE，
∴AE=AG-EG=DE-EG=DG．

点评：本题考查了实数的运算，分式的化简与求值，等腰三角形的判定与性质，平行四边形的性质．关键是明确实数混合运算的顺序，0指数，负整数指数，二次根式及特殊角的三角函数值，分式化简求值及分式有意义的条件．