题目内容
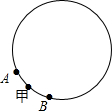
如图,A和B两个小机器人,自甲处同时出发相背而行,绕直径为整数米的圆周上运动,15分钟内相遇7次,如果A的速度每分钟增加6米,则A和B在15分钟内相遇9次,问圆周直径至多是多少米?至少是多少米?(取π=3.14)

由于圆的直径为D,则圆周长为πD.设A和B的速度和是每分钟v米,一次相遇所用的时间为
分;他们15分钟内相遇7次,用数学语言可以描述为8>
=
≥7①
如果A的速度每分钟增加6米,A加速后的两个机器人的速度和是每分钟(v+6)米,则A和B在15分钟内相遇9次,用数学语言可以描述为10>
=
≥9=2 ②
本题不是列方程,而是列不等式来描述题设的数量关系,这对一般学生可能比较生疏,体现了基本技能的灵活性.
由①,得-
<-
≤-
,由②,得
>
≥
,
上面两式相加,则有
>
>
,
>D>
,28.6624>D>9.55414,29>D>9.
已知“圆的直径为整数米”,所以,圆周直径至多是28米,至少是10米.
| πD |
| v |
| 15 | ||
|
| 15v |
| πD |
如果A的速度每分钟增加6米,A加速后的两个机器人的速度和是每分钟(v+6)米,则A和B在15分钟内相遇9次,用数学语言可以描述为10>
| 15 | ||
|
| 15(v+6) |
| πD |
本题不是列方程,而是列不等式来描述题设的数量关系,这对一般学生可能比较生疏,体现了基本技能的灵活性.
由①,得-
| 8π |
| 15 |
| v |
| D |
| 7π |
| 15 |
| 10π |
| 15 |
| v+6 |
| D |
| 9π |
| 15 |
上面两式相加,则有
| 3π |
| 15 |
| 6 |
| D |
| π |
| 15 |
| 90 |
| π |
| 30 |
| π |
已知“圆的直径为整数米”,所以,圆周直径至多是28米,至少是10米.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目