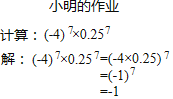题目内容
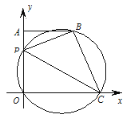
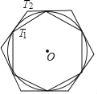
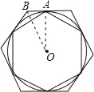
【题目】T1、T2分别为⊙O的内接正六边形和外切正六边形．设T1的半径r，T1、T2的边长分别为a、b，T1、T2的面积分别为S1、S2．下列结论：①r：a＝1：1；②r：b＝
；③a：b＝1：
；④S1：S2＝3：4．其中正确的有_____．（填序号）
【答案】①②④
【解析】
根据圆内接正六边形的半径等于它的边长，则r：a＝1：1；在由圆的半径和正六边形的半边以及正六边形的半径组成的直角三角形中，根据锐角三角函数即可求得其比值；
根据相似多边形的面积比是相似比的平方．可以求得其相似比，再进一步求得其面积比．
连接圆心O和T1的6个顶点可得6个全等的正三角形．
所以r：a＝1：1；故①正确；
连接圆心O和T2相邻的两个顶点，得以圆O半径为高的正三角形，
所以r：b＝AO：BO＝sin60°＝
：2；故②正确；
a：b＝
：2；故③错误；
T1：T2的边长比是：2，所以S1：S2＝（a：b）2＝3：4．故④正确；
故答案为：①②④
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
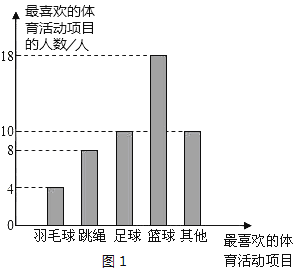
【题目】为了传承中华优秀传统文化，某校组织八年级学生参加了“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况，随机抽取了其中若干名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，绘制如下不完整的条形统计图.
汉字听写大赛成绩分数段统计表
分数段 | 频数 |
| 2 |
| 6 |
| 9 |
| 18 |
| 15 |
汉字听写大赛成绩分数段条形统计图
（1）补全条形统计图.
（2）这次抽取的学生成绩的中位数在________的分数段中；这次抽取的学生成绩在
的分数段的人数占抽取人数的百分比是_______.
（3）若该校八年级一共有学生350名，成绩在90分以上（含90分）为“优”，则八年级参加这次比赛的学生中成绩“优”等的约有多少人？
