题目内容
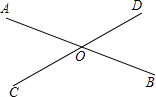如图，直线AB和CD相交于点O，若∠AOD=5∠AOC，则∠BOC=150°
150°
．分析：首先根据邻补角的性质可得∠AOD+∠AOC=180°，再把∠AOD=5∠AOC代入即可算出∠AOC的度数，进而算出∠AOD的度数，再根据对顶角相等可得答案．
解答：解：∵∠AOD+∠AOC=180°，
∠AOD=5∠AOC，
∴5∠AOC+∠AOC=180°，
∴∠AOC=30°，
∴∠AOD=5×30°=150°，
∴∠BOC=∠AOD=150°，
故答案为：150°．
∠AOD=5∠AOC，
∴5∠AOC+∠AOC=180°，
∴∠AOC=30°，
∴∠AOD=5×30°=150°，
∴∠BOC=∠AOD=150°，
故答案为：150°．
点评：此题主要考查了邻补角和对顶角，关键是掌握邻补角互补，对顶角相等．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
11、如图，直线AB和CD被直线MN所截，交点为E和F．则
27、如图，直线AB和CD相交于点O，EO⊥AB，垂足为O，OF平分∠BOD，求：
（2013•梧州一模）如图，直线AB和CD相交于点O，若∠AOD=55°，则∠AOC=（ ）