题目内容
【题目】当a、b、c为何值时,代数式 ![]() 有最小值?并求出这个最小值和此时以a、b、c值为边的三角形的面积.
有最小值?并求出这个最小值和此时以a、b、c值为边的三角形的面积.
【答案】解:∵ ![]()
= ![]() +b2﹣10b+25﹣25+c2﹣8c+16﹣16+6
+b2﹣10b+25﹣25+c2﹣8c+16﹣16+6
= ![]() +(b﹣5)2+(c﹣4)2﹣35,
+(b﹣5)2+(c﹣4)2﹣35,
∴ ![]() ≥0,(b﹣5)2≥0,(c﹣4)2≥0,
≥0,(b﹣5)2≥0,(c﹣4)2≥0,
∴代数式 ![]() 有最小值时,a=3,b=5,c=4,
有最小值时,a=3,b=5,c=4,
∴这个最小值为﹣35,
∴以a、b、c值为边的三角形为直角三角形,直角边为a和c ,
∴以a、b、c值为边的三角形的面积为12.
【解析】首先把 ![]() 进行配方得:
进行配方得: ![]() +b2﹣10b+25﹣25+c2﹣8c+16﹣16+6,进一步整理得:
+b2﹣10b+25﹣25+c2﹣8c+16﹣16+6,进一步整理得: ![]() +(b﹣5)2+(c﹣4)2﹣35,分析可知,
+(b﹣5)2+(c﹣4)2﹣35,分析可知, ![]() ≥0,(b﹣5)2≥0,(c﹣4)2≥0,即可推出最小值为﹣35,a=3,b=5,c=4,此时三角形为直角三角形直角边长度为4和3,所以面积为12.本题主要考查完全平方公式,非负数的性质,勾股定理的逆定理,关键在于利用完全平方公式对原代数式进行配方.分析a、b、c的值.
≥0,(b﹣5)2≥0,(c﹣4)2≥0,即可推出最小值为﹣35,a=3,b=5,c=4,此时三角形为直角三角形直角边长度为4和3,所以面积为12.本题主要考查完全平方公式,非负数的性质,勾股定理的逆定理,关键在于利用完全平方公式对原代数式进行配方.分析a、b、c的值.

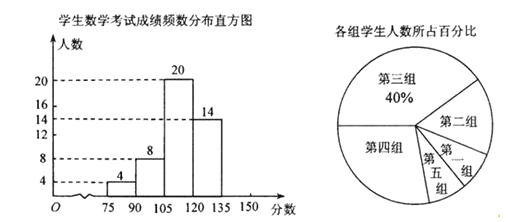
【题目】去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
组别 | 观点 | 频数 |
A | 大气气压低,空气不流动 | 120 |
B | 地面灰尘多,空气湿度低 | M |
C | 汽车尾气排放 | N |
D | 工厂造成的污染 | 180 |
E | 其它 | 90 |
请根据图表中提供的信息解答下列问题:
(1)填空:m、n等于多少?扇形统计图中E组所占百分比为多少?
(2)若该市人口约有75万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?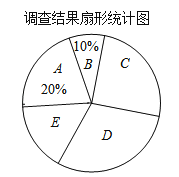
【题目】航模兴趣小组的老师想知道全组学生的年龄情况,于是让大家把自己的年龄写在纸上,下表是全组40名学生的年龄(单位:岁).
14 | 13 | 13 | 15 | 16 | 12 | 14 | 16 | 17 | 13 |
14 | 15 | 12 | 12 | 13 | 14 | 15 | 16 | 15 | 14 |
13 | 12 | 15 | 14 | 17 | 16 | 16 | 13 | 12 | 14 |
14 | 15 | 13 | 16 | 15 | 16 | 17 | 14 | 14 | 13 |
(1)在这个统计表中,13岁的频数是多少?频率是多少?
(2)多少岁的频率最大,这个最大频率是多少?
(3)假如老师随机地问一名学生的年龄,你认为老师最可能听到的回答是多少岁?