题目内容
已知△ABC的一边为5,另外两边恰是方程x2-6x+m=0的两个根.
(1)求实数m的取值范围.
(2)当m取最大值时,求△ABC的面积.
(1)求实数m的取值范围.
(2)当m取最大值时,求△ABC的面积.
分析:(1)根据韦达定理求得x1+x2=6,x1•x2,=m;然后由三角形的三边关系、一元二次方程的根的判别式列出关于m的不等式组,解不等式即可;
(2)过点A作AD⊥BC于点D.在直角三角形ACD中,利用勾股定理求得AD的长度.然后利用三角形的面积公式:面积=
底×高,解答问题.
(2)过点A作AD⊥BC于点D.在直角三角形ACD中,利用勾股定理求得AD的长度.然后利用三角形的面积公式:面积=
| 1 |
| 2 |
解答:解:(1)设另两边为x1,x2,且x1>x2.
∴由韦达定理,得
x1+x2=6,x1•x2,=m;
根据三边关系得:
x1+x2=6>5 ①;
∴x1-x2=
=
<5;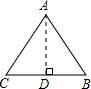
解得,m>
;
又∵△=36-4m≥0,
解得,m≤9,
∴m的取值范围是:
<m≤9;
(2)当m取最大值,即m=9时,由原方程得
x2-6x+9=0,即(x-3)2=0,
解得,x1=x2=3,
过点A作AD⊥BC于点D.
∴AD=
∴S△ABC=
.
∴由韦达定理,得
x1+x2=6,x1•x2,=m;
根据三边关系得:
x1+x2=6>5 ①;
∴x1-x2=
| (x1+x2)2-4x1x2 |
| 36-4m |

解得,m>
| 11 |
| 2 |
又∵△=36-4m≥0,
解得,m≤9,
∴m的取值范围是:
| 11 |
| 2 |
(2)当m取最大值,即m=9时,由原方程得
x2-6x+9=0,即(x-3)2=0,
解得,x1=x2=3,
过点A作AD⊥BC于点D.
∴AD=
| ||
| 2 |
∴S△ABC=
5
| ||
| 4 |
点评:本题综合考查了三角形的三边关系、根的判别式、根与系数的关注.将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
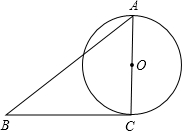 如图已知△ABC的一边BC与以AC为直径的⊙O相切于点C,若BC=4,AB=5,则sinB=
如图已知△ABC的一边BC与以AC为直径的⊙O相切于点C,若BC=4,AB=5,则sinB=