题目内容
已知△ABC的一边AC为关于x的一元二次方程x2+mx+4=0的两个正整数根之一,且另两边长为BC=4,AB=6,求cosA.分析:根据题意画出图形,根据根与系数的关系求出一元二次方程x2+mx+4=0的两根之积,由方程的两个正整数根估计出两根的值,再根据三角形的三边关系确定出AC的长,由等腰三角形的性质可求出AD的长,最后由锐角三角函数的定义解答即可.
解答: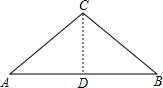 解:根据与系数的关系可知:
解:根据与系数的关系可知:
x1•x2=4,
又∵x1、x2为正整数解,
∴x1,x2可为1、4或2、2(2分)
又∵BC=4,AB=6,
∴2<AC<10,
∴AC=4,(5分)
∴AC=BC=4,△ABC为等腰三角形,
过点C作CD⊥AB,∴AD=3,(7分)
cosA=
=
.(8分)
 解:根据与系数的关系可知:
解:根据与系数的关系可知:x1•x2=4,
又∵x1、x2为正整数解,
∴x1,x2可为1、4或2、2(2分)
又∵BC=4,AB=6,
∴2<AC<10,
∴AC=4,(5分)
∴AC=BC=4,△ABC为等腰三角形,
过点C作CD⊥AB,∴AD=3,(7分)
cosA=
| AD |
| AC |
| 3 |
| 4 |
点评:本题考查的是锐角三角函数的定义、一元二次方程根与系数的关系及等腰三角形的性质,涉及面较广,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
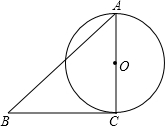 如图,已知△ABC的一边BC与以AC为直径的⊙O相切于点C,若BC=4,AB=5,则cosB=
如图,已知△ABC的一边BC与以AC为直径的⊙O相切于点C,若BC=4,AB=5,则cosB= 已知△ABC的一边AC为关于x的一元二次方程x2+mx+5=0的两个正整数根之一,且另两边长为BC=3,AB=5,求cosA.
已知△ABC的一边AC为关于x的一元二次方程x2+mx+5=0的两个正整数根之一,且另两边长为BC=3,AB=5,求cosA.