Question

【题目】如图，四边形ABCD内接于⊙O，点E在CB的延长线上，连接AC，AE，∠ACB=∠BAE=45°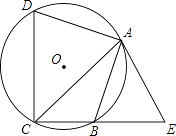

（1）求证：AE是⊙O的切线；
（2）若 AB=AD，AC=2 ，tan∠ADC=3，求CD的长．

Answer 1

【答案】
（1）

证明：

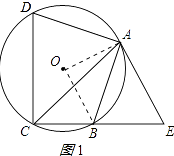
连接OA、OB，如图1所示：

∵∠ACB=45°，

∴∠AOB=2∠ACB=90°，

∵OA=OB，

∴∠OAB=∠OBA=45°，

∵∠BAE=45°，

∴∠OAE=∠OAB+∠BAE=90°，

∴AE⊥OA，

∴AE是⊙O的切线

（2）

解：

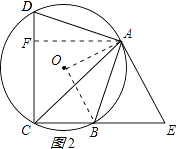
作AF⊥CD于F，如图2所示：

∵AB=AD，

∴ ，

∴∠ACB=∠ACD=45°，

∵AF⊥CD，

∴∠AFC=∠AFD=90°，

∵AC=2 ，

∴在Rt△AFC中，AF=CF=ACsin∠ACF=2 × =2，

∵在Rt△AFD中，tan∠ADC= =3，

∴DF= ，

∴CD=CF+DF=2+ = ．

【解析】（1）连接OA、OB，由圆周角定理得出∠AOB=2∠ACB=90°，由等腰直角三角形的性质得出∠OAB=∠OBA=45°，求出∠OAE=∠OAB+∠BAE=90°，即可得出结论；（2）作AF⊥CD于F，证出 ，由圆周角定理得出∠ACB=∠ACD=45°，由三角函数求出AF=CF=ACsin∠ACF=2，DF= ，即可得出CD的长．
【考点精析】认真审题，首先需要了解切线的判定定理(切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线)．