题目内容
【题目】在平面直角坐标系中,B点坐标为(x、y),且x、y满足|x+y﹣8|+(x﹣y)2=0.
(1)求B点坐标;
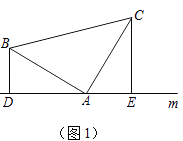
(2)如图,点A为y轴正半轴上一点,过点B作BC⊥AB,交x轴正半轴于点C,求证:AB=BC. 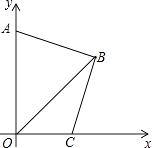
【答案】
(1)解:∵|x+y﹣8|+(x﹣y)2=0,
∴ ![]() ,
,
解得, ![]() ,
,
即点B的坐标为(4,4)
(2)解:作BD⊥OA于点D,作BE⊥OC于点E,如右图所示,
∵BC⊥AB,∠DBE=90°,∠ADB=∠CEB=90°,
∴∠ABC=90°,
∴∠ABD+∠DBC=∠DBC+∠CBE=90°,
∴∠ABD=∠CBE,
又∵点B(4,4),
∴BD=BE=4,
∴△ADB≌△CEB(ASA),
∴AB=BC.
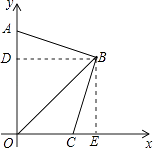
【解析】(1)根据x、y满足|x+y﹣8|+(x﹣y)2=0,可以求得x、y的值,从而可以求得点B的坐标;(2)根据题意,可以作辅助线,只要证明△ADB≌△CEB即可证明AB与BC的关系,根据题目中的条件可以得到△ADB≌△CEB的条件,本题得以解决.
【考点精析】掌握解二元一次方程组是解答本题的根本,需要知道二元一次方程组:①代入消元法;②加减消元法.

练习册系列答案
相关题目