题目内容
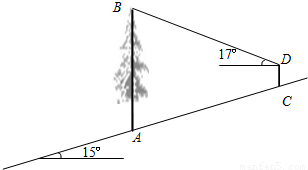
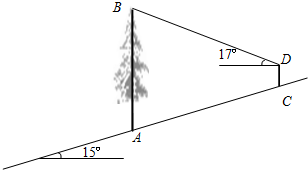 如图,在山坡上有一棵大树AB,小明在坡上的C点处测得树顶B的仰角为17°,已知山坡的坡角为15°,测角仪高CD为1.5米,测角仪离大树的坡面距离AC为50米,求大树AB的高.(精确到0.1米)
如图,在山坡上有一棵大树AB,小明在坡上的C点处测得树顶B的仰角为17°,已知山坡的坡角为15°,测角仪高CD为1.5米,测角仪离大树的坡面距离AC为50米,求大树AB的高.(精确到0.1米)
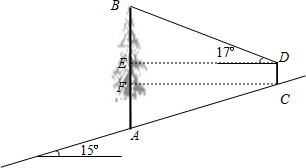 解:作DE⊥AB于E,CF⊥AB于F,得矩形DEFC
解:作DE⊥AB于E,CF⊥AB于F,得矩形DEFC∴EF=CD=1.5,由已知得,∠FCA=15°
在Rt△ACF中,∠AFC=90°
AF=AC•sin∠ACF=50×sin15°≈12.94
CF=AC•cos∠ACF=50×cos15°≈48.30
在Rt△DBE中,∠BED=90°
BE=DE•tan∠BDE=48.30×tan17°≈14.77
∴AB=BE+EF+AF=12.94+1.5+14.77≈29.2
答:大树AB的高约为29.2米.
分析:作DE⊥AB于E,CF⊥AB于F,得矩形DEFC,因为AF,CF,DE,BE在直角三角形中,知道仰角的度数,可求出直角三角形中其他角的度数,用三角函数可分别2.求出线段的长,从而求得树高.
点评:本题考查解直角三角形的应用,俯角仰角问题和坡度坡角问题,关键是熟记角的坡度的概念,准确找出角然后作出辅助线,利用三角函数求解.

练习册系列答案
相关题目
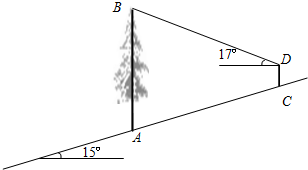 24、如图,在山坡上有一棵大树AB,小明在坡上的C点处测得树顶B的仰角为17°,已知山坡的坡角为15°,测角仪高CD为1.5米,测角仪离大树的坡面距离AC为50米,求大树AB的高.(精确到0.1米)
24、如图,在山坡上有一棵大树AB,小明在坡上的C点处测得树顶B的仰角为17°,已知山坡的坡角为15°,测角仪高CD为1.5米,测角仪离大树的坡面距离AC为50米,求大树AB的高.(精确到0.1米) (2012•吴中区二模)2012年4月11曰16时38分北苏门答腊西海岸发生里氏8.6级地震,并伴有海啸.山坡上有一棵与水平面垂直的大树,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=6m.
(2012•吴中区二模)2012年4月11曰16时38分北苏门答腊西海岸发生里氏8.6级地震,并伴有海啸.山坡上有一棵与水平面垂直的大树,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=6m. (2012•南宁)如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为6
(2012•南宁)如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为6