题目内容
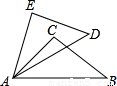
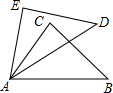 如图,已知AE=AC,AD=AB,∠EAD=∠CAB,求证:∠B=∠D.
如图,已知AE=AC,AD=AB,∠EAD=∠CAB,求证:∠B=∠D.
证明:∵∠EAC=∠DAB,
∴∠EAC+∠CAD=∠DAB+∠CAD,
∴∠EAD=∠CAB,
又∵AE=AC,AD=AB,
∴△EAD≌△CAB,
∴∠B=∠D.
分析:三角形全等条件中必须是三个元素,我们只要能证明∠EAD=∠CAB这一条件可用SAS判定两个三角形全等,再利用全等三角形的性质:对应角相等问题得证.
点评:本题考查了全等三角形的判定;由∠EAC=∠DAB得出∠EAD=∠CAB是正确解决问题的关键,这种方法在三角形全等的证明中经常用到.
∴∠EAC+∠CAD=∠DAB+∠CAD,
∴∠EAD=∠CAB,
又∵AE=AC,AD=AB,
∴△EAD≌△CAB,
∴∠B=∠D.
分析:三角形全等条件中必须是三个元素,我们只要能证明∠EAD=∠CAB这一条件可用SAS判定两个三角形全等,再利用全等三角形的性质:对应角相等问题得证.
点评:本题考查了全等三角形的判定;由∠EAC=∠DAB得出∠EAD=∠CAB是正确解决问题的关键,这种方法在三角形全等的证明中经常用到.

练习册系列答案
相关题目
 26、如图,已知AE=AC,AD=AB,∠EAC=∠DAB.求证:△EAD≌△CAB.
26、如图,已知AE=AC,AD=AB,∠EAC=∠DAB.求证:△EAD≌△CAB. 如图,已知AE=AC,AD=AB,∠EAD=∠CAB,求证:∠B=∠D.
如图,已知AE=AC,AD=AB,∠EAD=∠CAB,求证:∠B=∠D.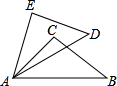 如图,已知AE=AC,AD=AB,∠EAC=∠DAB.求证:△EAD≌△CAB.
如图,已知AE=AC,AD=AB,∠EAC=∠DAB.求证:△EAD≌△CAB.