题目内容
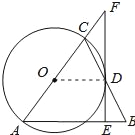
【题目】如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线EF,交AB和AC的延长线于E、F.
(1)求证:FE⊥AB;
(2)当AE=6,sin∠CFD=![]() 时,求EB的长.
时,求EB的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)先证明OD∥AB,得出∠ODF=∠AEF,再由切线的性质得出∠ODF=90°,证出∠AEF=90°,即可得出结论;
(2)设OA=OD=OC=r,先由三角函数求出AF,再证明△ODF∽△AEF,得出对应边成比例求出半径,得出AB,即可求出EB.
(1)证明:连接OD,如图所示:
∵OC=OD,
∴∠OCD=∠ODC,
∵AB=AC,
∴∠ACB=∠B,
∴∠ODC=∠B,
∴OD∥AB,
∴∠ODF=∠AEF,
∵EF与⊙O相切,
∴OD⊥EF,
∴∠ODF=90°,
∴∠AEF=∠ODF=90°,
∴EF⊥AB;
(2)解:设OA=OD=OC=r,
由(1)知:OD∥AB,OD⊥EF,
在Rt△AEF中,sin∠CFD=![]() ,AE=6,
,AE=6,
∴AF=10,
∵OD∥AB,
∴△ODF∽△AEF,
∴![]()
∴![]()
解得r=![]() ,
,
∴AB=AC=2r=![]() ,
,
∴EB=AB﹣AE=![]() ﹣6=
﹣6=![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目