题目内容
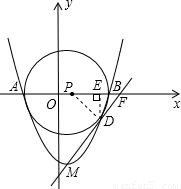
(2007•盐城)如图,已知抛物线y=a(x-1)2- 与x轴交于A、B两点(点A在左边),且过点D(5,-3),顶点为M,直线MD交x轴于点F.
与x轴交于A、B两点(点A在左边),且过点D(5,-3),顶点为M,直线MD交x轴于点F.(1)求a的值;
(2)以AB为直径画⊙P,问:点D在⊙P上吗?为什么?
(3)直线MD与⊙P存在怎样的位置关系?请说明理由.

【答案】分析:(1)将D(5,-3)代入解析式即可求出a的值;
(2)求出⊙P的半径,计算出PD的长,与半径比较即可判断点D是否在⊙P上;
(3)由于MD经过半径的外端,通过勾股定理的逆定理判断出∠PDF=90°即可直线MD与⊙P相切.
解答:解:(1)把D(5,-3)代入y=a(x-1)2- ,
,
得:a= .(2分)
.(2分)
(2)y= (x-1)2-
(x-1)2-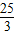 ,
,
令y=0,得:x1=-4,x2=6,
∴A(-4,0),B(6,0),
∴AB=10.(4分)
∵AB为⊙P的直径,
∴P(1,0),
∴⊙P的半径r=5(5分)
过点D作DE⊥x轴于点E,则E(5,0).
∴PE=5-1=4,DE=3,
∴PD=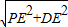 =5,(6分)
=5,(6分)
∴PD与⊙P的半径相等,
∴点D在⊙P上.(7分)
(3)设直线MD的函数解析式为:y=kx+b(k≠0)
把M(1,-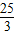 ),D(5,-3)代入
),D(5,-3)代入
得: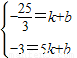 ,
,
∴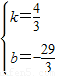 ,
,
∴直线MD的函数解析式为:y= x-
x-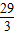 .(8分)
.(8分)
设直线MD与x轴交于点F,
令y=0则0= x-
x-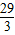 ,
,
得x=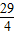 .
.
∴F(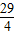 ,0),(9分)
,0),(9分)
∴EF=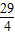 -5=
-5= ,
,
∴DF2=EF2+DE2=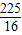 ,
,
PF2=(OF-OP)2=(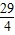 -1)2=
-1)2=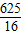 ,
,
DP2=25,
∴DP2+DF2=PF2
∴FD⊥DP,(11分)
又∵点D在⊙P上,
∴直线MD与⊙P相切.(12分)
点评:此题是一道结论开放性题目,考查了点和圆的位置关系、直线和圆的位置关系,通过函数解析式求出相应点的坐标及线段的长,是解答此题的必要环节.
(2)求出⊙P的半径,计算出PD的长,与半径比较即可判断点D是否在⊙P上;
(3)由于MD经过半径的外端,通过勾股定理的逆定理判断出∠PDF=90°即可直线MD与⊙P相切.
解答:解:(1)把D(5,-3)代入y=a(x-1)2-
 ,
,得:a=
 .(2分)
.(2分)(2)y=
 (x-1)2-
(x-1)2-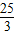 ,
,令y=0,得:x1=-4,x2=6,
∴A(-4,0),B(6,0),
∴AB=10.(4分)
∵AB为⊙P的直径,
∴P(1,0),
∴⊙P的半径r=5(5分)
过点D作DE⊥x轴于点E,则E(5,0).
∴PE=5-1=4,DE=3,
∴PD=
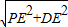 =5,(6分)
=5,(6分)∴PD与⊙P的半径相等,
∴点D在⊙P上.(7分)

(3)设直线MD的函数解析式为:y=kx+b(k≠0)
把M(1,-
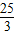 ),D(5,-3)代入
),D(5,-3)代入得:
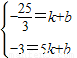 ,
,∴
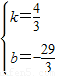 ,
,∴直线MD的函数解析式为:y=
 x-
x-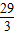 .(8分)
.(8分)设直线MD与x轴交于点F,
令y=0则0=
 x-
x-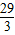 ,
,得x=
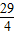 .
.∴F(
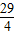 ,0),(9分)
,0),(9分)∴EF=
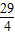 -5=
-5= ,
,∴DF2=EF2+DE2=
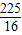 ,
,PF2=(OF-OP)2=(
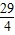 -1)2=
-1)2=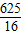 ,
,DP2=25,
∴DP2+DF2=PF2
∴FD⊥DP,(11分)
又∵点D在⊙P上,
∴直线MD与⊙P相切.(12分)
点评:此题是一道结论开放性题目,考查了点和圆的位置关系、直线和圆的位置关系,通过函数解析式求出相应点的坐标及线段的长,是解答此题的必要环节.

练习册系列答案
相关题目
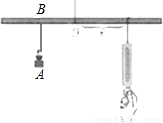
(2007•盐城)如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
| x(cm)…10 | 15 | 20 | 25 30… |
| y(N)…30 | 20 | 15 | 12 10… |
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?


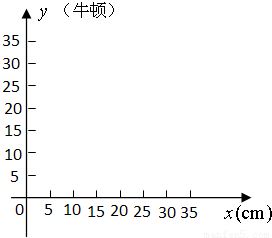
(2007•盐城)如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
| x(cm)…10 | 15 | 20 | 25 30… |
| y(N)…30 | 20 | 15 | 12 10… |
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?


(2007•盐城)如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
| x(cm)…10 | 15 | 20 | 25 30… |
| y(N)…30 | 20 | 15 | 12 10… |
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?


(2007•盐城)如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?


| x(cm)…10 | 15 | 20 | 25 30… |
| y(N)…30 | 20 | 15 | 12 10… |
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?


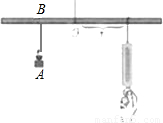
(2007•盐城)如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
| x(cm)…10 | 15 | 20 | 25 30… |
| y(N)…30 | 20 | 15 | 12 10… |
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?

