题目内容
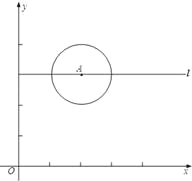
【题目】如图,已知O为坐标原点,点A的坐标为(2,3),⊙A的半径为1,过A作直线l平行于x轴,点P在l上运动.
(1)当点P运动到圆上时,求线段OP的长.
(2)当点P的坐标为(4,3)时,试判断直线OP与⊙A的位置关系,并说明理由.
【答案】(1)![]() ;(2)直线OP与⊙A相离,详见解析.
;(2)直线OP与⊙A相离,详见解析.
【解析】
(1)要注意考虑两种情况,根据勾股定理计算其距离;
(2)根据相似三角形的性质求得圆心到直线的距离,再进一步根据数量关系判断其位置关系.
解:(1)如图,设l与y轴交点为C.
当点P运动到圆上时,有P1、P2两个位置,
∴![]() ;
;
![]() .
.
(2)连接OP,过点A作AM⊥OP,垂足为M.
∵P(4,3),
∴CP=4,AP=2.
在Rt△OCP中
![]() .
.
∵∠APM=∠OPC,∠PMA=∠PCO=90°,
∴△PAM∽△POC.
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴直线OP与⊙A相离.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
【题目】如下表,方程1、方程2、方程3…是按照一定规律排列的一列方程。
(1)猜想方程1的解,并将它们的解填在表中的空白处。
序号 | 方程 | 方程的解( |
1 |
|
|
2 |
|
|
3 |
|
|
… | …… | …… |
(2)若方程![]()
![]() 的解是
的解是![]() ,猜想a,b的值。
,猜想a,b的值。
(3)请写出这列方程中的第n个方程和它的解。