题目内容
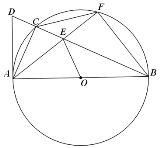
【题目】如图,△ABC是⊙O内接三角形,AB是⊙O的直径,C是弧AF的中点,弦BC,AF相交于点E,在BC延长线上取点D,使得AD=AE.
(1)求证:AD是⊙O切线;
(2)若∠OEB=45°,求sin∠ABD的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)本题考查切线的证明,总体思路是“证垂直以及半径”,根据题干AB为直径,此处考查圆周角定理的运用;根据C是弧的中点,此处考查同弧所对的圆周角相等,综合以上通过直角互余以及角的互换解答本题.
(2)本题考查圆周角定理以及正弦三角函数综合运用,需要通过弧等推角等,边等推角等,结合图形特点选取合适的三角形进行角的互换,进一步推出边的关系解答此题.
(1)∵AB是⊙O的直径
∴∠ACB=90°.
∴∠CBA+∠CAB=90°.
又∵AD=AE,
∴∠CAD=∠CAE.
∵C是![]() 的中点,
的中点,
∴![]()
∴∠CAE=∠CBA.
∴∠CAD+∠CAB=90°.
∴OA⊥DA.
又∵OA是⊙O的半径,
∴DA是⊙O的切线.
(2)∵C是![]() 的中点,
的中点,
∴![]()
∴∠CBF=∠CBA.
设∠CBF=∠CBA=x,∠FAB=y.
∵AB是⊙O的直径,
∴∠AFB=90°.
∴y+2x=90°,y=90°-2x.
∵∠FEB=y+x,
∴∠AEO=180°-∠OEB-∠FEB
=180°-45°-y-x
=135°-x-y
=135°-x-(90°-2x)
=45°+x,
又∵∠AOE=∠OBE+∠OEB=45°+x,
∴∠AEO=∠AOE.
∴AE=AO.
∵∠ACB=∠ACB,∠CAE=∠CBA,
∴△CEA∽△CAB.
∴![]() .
.
∴![]() ,
,![]()
∴![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目