题目内容
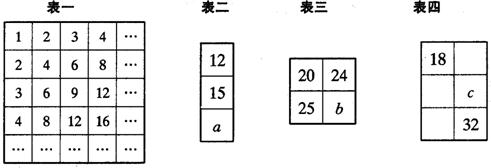
观察表一,寻找规律.表二、表三分别是从表一中选取的一部分,则a=
=
.
表一
表二
表三
17
17
,| a+b |
| 2 |
| 37 |
| 2 |
| 37 |
| 2 |
表一
| 0 | 1 | 2 | 3 | … |
| 1 | 3 | 5 | 7 | … |
| 2 | 5 | 8 | 11 | … |
| 3 | 7 | 11 | 15 | … |
| … | … | … | … | … |
| 11 |
| 14 |
| a |
| 11 | 13 |
| 17 | b |
分析:根据表(2)中11和14的位置可以得到,11所在的行一定是第一行,则14是在第二行,a在第三行,根据表(1)可以得到:下一行的数总是与对应的上一行的数的差是下一行的行的序号,则a比14大3,则a即可求解;
根据表(1)可以得到在同一行中相邻的两个数,后边的数与前边的数的差也是这一行的行的序号,在表三中,13-11=2,则11所在的行是第二行,则17与b所在的行是第三行,因而可以求得b=17+3,则代数式的值即可求得.
根据表(1)可以得到在同一行中相邻的两个数,后边的数与前边的数的差也是这一行的行的序号,在表三中,13-11=2,则11所在的行是第二行,则17与b所在的行是第三行,因而可以求得b=17+3,则代数式的值即可求得.
解答:解:a=14+3=17,b=17+3=20
则
=
.
故答案是:17,
.
则
| a+b |
| 2 |
| 37 |
| 2 |
故答案是:17,
| 37 |
| 2 |
点评:考查了规律型:数字的变化,此题的关键是找规律,正确理解前后的两个数或上下的两个数之间的关系与行号的联系是关键.

练习册系列答案
相关题目