题目内容
(2005•锦州)如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=4,S2=8,则AB的长为 .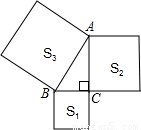
【答案】分析:先利用正方形的面积公式分别求出正方形S1、S2的边长即AC、BC的长,在Rt△ABC中,已知AC、BC的长,利用勾股定理求斜边AC.
解答:解:∵S1=4,∴BC2=4,
∵S2=8,∴AC2=8,
∴在Rt△ABC中,BC2+AC2=AB2,
∴AB=2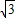 .
.
点评:考查正方形的面积公式及勾股定理的应用.
解答:解:∵S1=4,∴BC2=4,
∵S2=8,∴AC2=8,
∴在Rt△ABC中,BC2+AC2=AB2,
∴AB=2
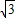 .
.点评:考查正方形的面积公式及勾股定理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
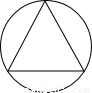
(2005•锦州)如图,小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则该圆的半径为( )
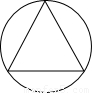
A.3 cm
cm
B.3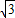 cm
cm
C.4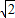 cm
cm
D.4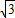 cm
cm

A.3
 cm
cmB.3
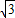 cm
cmC.4
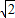 cm
cmD.4
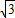 cm
cm
 cm
cm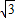 cm
cm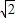 cm
cm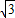 cm
cm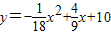 .
.