题目内容
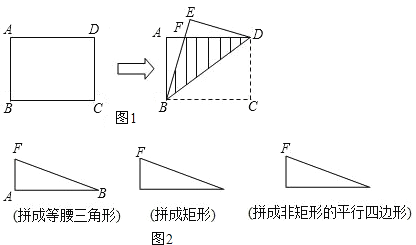
【题目】已知:如图1,把一张矩形纸片ABCD沿对角线BD折叠,将重合部分(△BFD)剪去,得到△ABF和△EDF.
(1)求证:FB=FD;
(2)求证:△ABF≌△EDF;
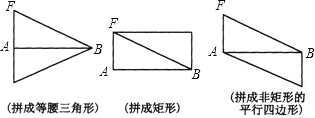
(3)将△ABF与△EDF不重合地拼在一起,可拼成特殊三角形和特殊四边形,请你按照下列要求将拼图补画完整(图2).
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】(1)根据翻折的性质得出∠FBD=∠DBC,再利用平行线的性质证明即可;
(2)由折叠的性质求证△ABF≌△EFD;
(3)根据题意要求作图即可.
(1)证明:由折叠的性质知,∠FBD=∠DBC,
∵矩形ABCD,
∴AD∥BC,
∴∠FDB=∠DBC,
∴∠FBD=∠FDB,
∴FB=FD;
(2)证明:由折叠的性质知,ED=CD=AB,
又∵∠E=∠A=90°,∠EFD=∠AFB,
∴△ABF≌△EFD;
(3)如图,

 阅读快车系列答案
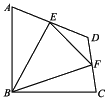
阅读快车系列答案【题目】如图,在四边形ABCD中,∠ABC=90°,AB=BC=2![]() ,E,F分别是AD,CD的中点,连结BE,BF,EF.若四边形ABCD的面积为6,则△BEF的面积为( )
,E,F分别是AD,CD的中点,连结BE,BF,EF.若四边形ABCD的面积为6,则△BEF的面积为( )
A. 2B. ![]() C.
C. ![]() D. 3
D. 3
【题目】近年来,越来越多的人们加入到全民健身的热潮中来.“健步走”作为一项行走速度和运动量介于散步和竞走之间的步行运动,因其不易发生运动伤害,不受年龄、时间和场地限制的优点而受到人们的喜爱.随着信息技术的发展,很多手机![]() 可以记录人们每天健步走的步数,为大家的健身做好记录.
可以记录人们每天健步走的步数,为大家的健身做好记录.
小明的爸爸妈妈都是健步走爱好者,一般情况下,他们每天都会坚持健步走.小明为了给爸爸妈妈颁发4月份的“运动达人”奖章,进行了抽样调查,过程如下,请补充完整.
从4月份随机抽取10天,记录爸爸妈妈运动步数(千步)如下:
爸爸12 10 11 15 14 13 14 11 14 12
妈妈11 14 15 2 11 11 14 15 14 14
根据以上信息,整理分析数据如下表所示:
平均数 | 中位数 | 众数 | |
爸爸 | 12.6 | 12.5 |
|
妈妈 |
| 14 | 14 |
(1)直接在下面空白处写出表格中![]() ,
,![]() 的值;
的值;
(2)你认为小明会把4月份的“运动达人”奖章颁发给谁,并说明理由.