题目内容
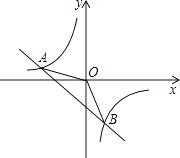
【题目】如图,顶点为A( ![]() ,1)的抛物线经过坐标原点O,与x轴交于点B.
,1)的抛物线经过坐标原点O,与x轴交于点B.
(1)求抛物线对应的二次函数的表达式;
(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;
(3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.
【答案】
(1)
解:∵抛物线顶点为A( ![]() ,1),
,1),
设抛物线解析式为y=a(x﹣ ![]() )2+1,
)2+1,
将原点坐标(0,0)在抛物线上,
∴0=a( ![]() )2+1
)2+1
∴a=﹣ ![]() .
.
∴抛物线的表达式为:y=﹣ ![]() x2+
x2+ ![]() x
x
(2)
解:令y=0,得 0=﹣ ![]() x2+
x2+ ![]() x,
x,
∴x=0(舍),或x=2 ![]()
∴B点坐标为:(2 ![]() ,0),
,0),
设直线OA的表达式为y=kx,
∵A( ![]() ,1)在直线OA上,
,1)在直线OA上,
∴ ![]() k=1,
k=1,
∴k= ![]() ,
,
∴直线OA对应的一次函数的表达式为y= ![]() x.
x.
∵BD∥AO,
设直线BD对应的一次函数的表达式为y= ![]() x+b,
x+b,
∵B(2 ![]() ,0)在直线BD上,
,0)在直线BD上,
∴0= ![]() ×2
×2 ![]() +b,
+b,
∴b=﹣2,
∴直线BD的表达式为y= ![]() x﹣2.
x﹣2.
由 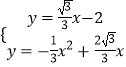
得交点D的坐标为(﹣ ![]() ,﹣3),
,﹣3),
令x=0得,y=﹣2,
∴C点的坐标为(0,﹣2),
由勾股定理,得:OA=2=OC,AB=2=CD,OB=2 ![]() =OD.
=OD.
在△OAB与△OCD中,
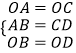 ,
,
∴△OAB≌△OCD.
(3)
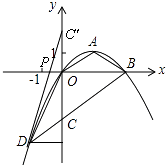
解:点C关于x轴的对称点C'的坐标为(0,2),
∴C'D与x轴的交点即为点P,它使得△PCD的周长最小.
过点D作DQ⊥y,垂足为Q,
∴PO∥DQ.
∴△C'PO∽△C'DQ.
∴ ![]() ,
,
∴ ![]() ,
,
∴PO= ![]() ,
,
∴点P的坐标为(﹣ ![]() ,0)
,0)
【解析】(1)用待定系数法求出抛物线解析式,(2)先求出直线OA对应的一次函数的表达式为y= ![]() x.再求出直线BD的表达式为y=
x.再求出直线BD的表达式为y= ![]() x﹣2.最后求出交点坐标C,D即可;(3)先判断出C'D与x轴的交点即为点P,它使得△PCD的周长最小.作辅助线判断出△C'PO∽△C'DQ即可.
x﹣2.最后求出交点坐标C,D即可;(3)先判断出C'D与x轴的交点即为点P,它使得△PCD的周长最小.作辅助线判断出△C'PO∽△C'DQ即可.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.